The resistance in the gap of a metre bridge is 10Ω and the balance point 40 Cm from the left end .Calculate the value of unknwon resistance .
R2=12=l99−l gives l=33cm
But we read the lengths as l=33 cm and 100-33 = 67 cm and write RS=3367=0.4925
Now , then we interchange the resistances, we should have RS=21=l99−l which gives l=66 cm - But we read lengths as l=66 cm and 100 - 66 = 32 cm and write RS=6634 or R/S = (34)/(66)=0.5152is0.5038andisveryclose→1/2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-1)
17 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
The resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
View SolutionWith two resistance R1andR2(>R1) in the two gaps of a metre bridge the balance was found to be 1/3 m from the zero end. When a 6Ωresistance is connected in series with the smaller of the two resistance, the point is shifted to 2/3 m from the same end, then R1andR2 are
View Solution
Knowledge Check
When a metal conductor connected to left gap of a meter bridge is heated, the balancing point
Ashifts towards rightBshifts towards leftCremains unchangedDremains at zeroTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
A3B6C9D12
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
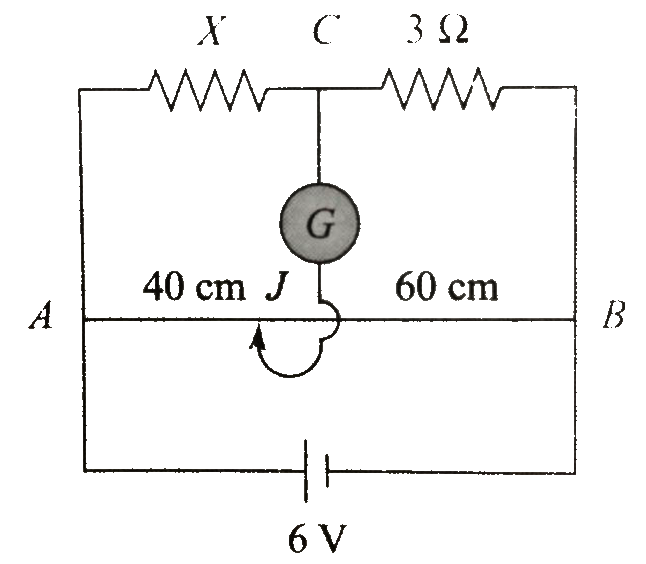
View SolutionIn the circuit shows in Fig. 6.20, a meter bridge is in its balance state. The meter bridge wire has a resistance of 1Ωcm−1. Calculate the value of the unknow resistance X and current drawn from the battery of negligible internal resistance.
View SolutionTwo resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View SolutionWhen un known resistance and a resistance of 4Ω are used in the left and right gaps of a meter bridge, the balance point is 50cm. the shift in the balance point if a 4Ω resistance is now connected parallel to the resistor in right gap ______
View SolutionTwo unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View Solution
