Two metal strips, each of length, each of length l, are clamped parallel to each other on a horizontal floor with a separation b between them. A wire of mass m line on them perpendicularly as shown in figure. A vertically upward magnetic field of strenght B exists in the space. The matal strips are smooth but the cofficient of freiction between the wire and the floor is μ. A current i is established when the switch S is closed at the instant t=0. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?

When current starts flowing in the wire, it experiences a force, F =Bib of constant magnitude due to which it accelerates on the metal strips. There after when wire falls on the floor, it retards due to friction and finally stops. Thus
a=Fm=Bibm
The velocity gained by the wire on the strips
v2=0+2al=2Biblm
Let x be the distance moved by the wire on the floor.
Its final velocity becomes zero, and so
=v2−2a.xorx=v22a.
Here a.=μmgm=μg
∴x=[2Biblm]2μg=Biblμmg
Note : Try usiing work - energy theorem
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
5 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
6 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A wire of infinite length bent as shown in figure carries current l. What is the magnetic field at the point P ?
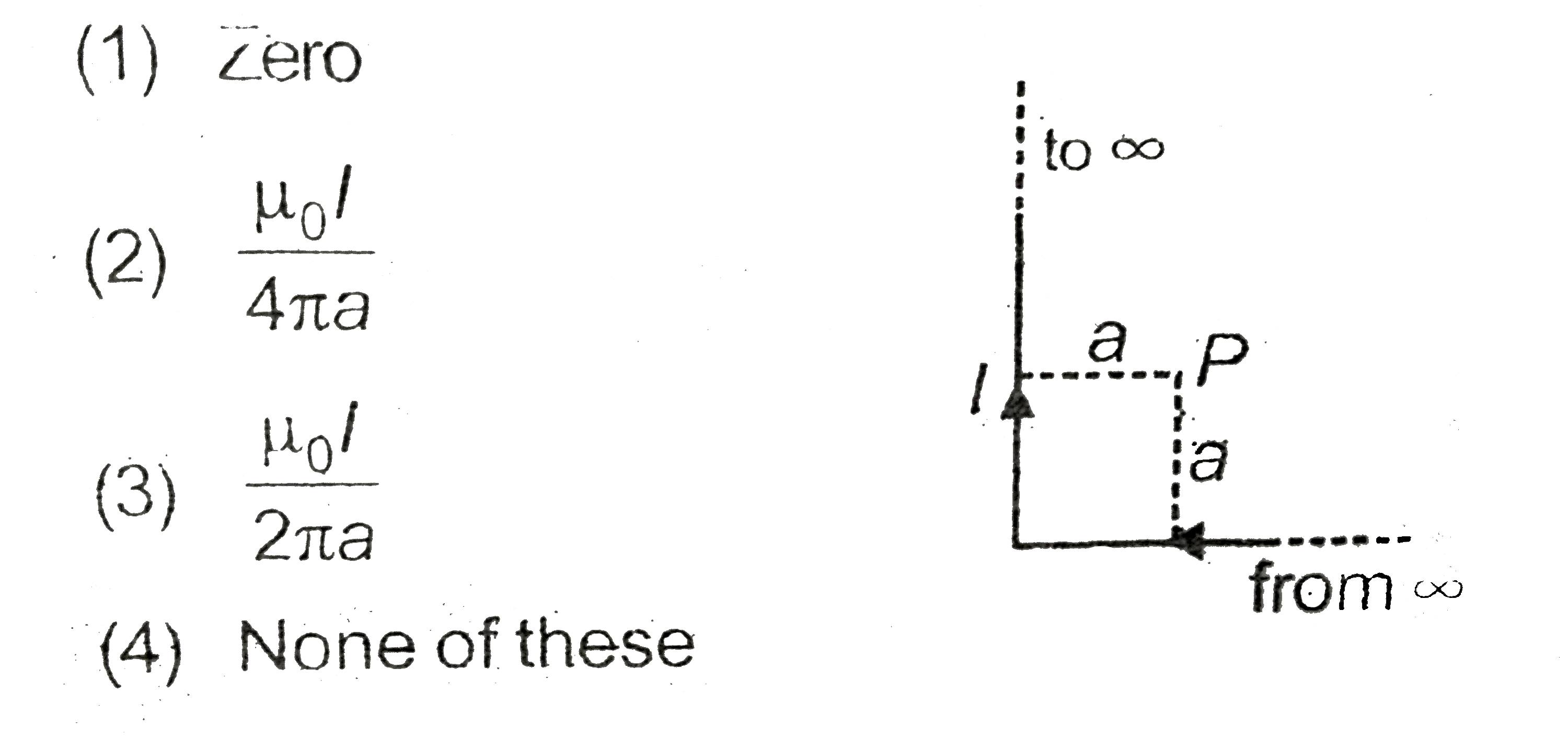
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionTwo thin long wires are parallel to each other at a separation d apart and they carry equal currents l each along the same direction as shown in figure. The magnetic field (B) at a point P varieswith x according to graph.
_PHY_E06_274_Q01.png)
View SolutionA conducting stick of length 2L and mass m is moving down a smooth inclined plane of inclination 60∘ with constant speed 5m/s. A current 2A is flowing in the conductor perpendicular to the paper inwards. A vertically upward magnetic field B exists in space there. The magnitude of magnetic field B is
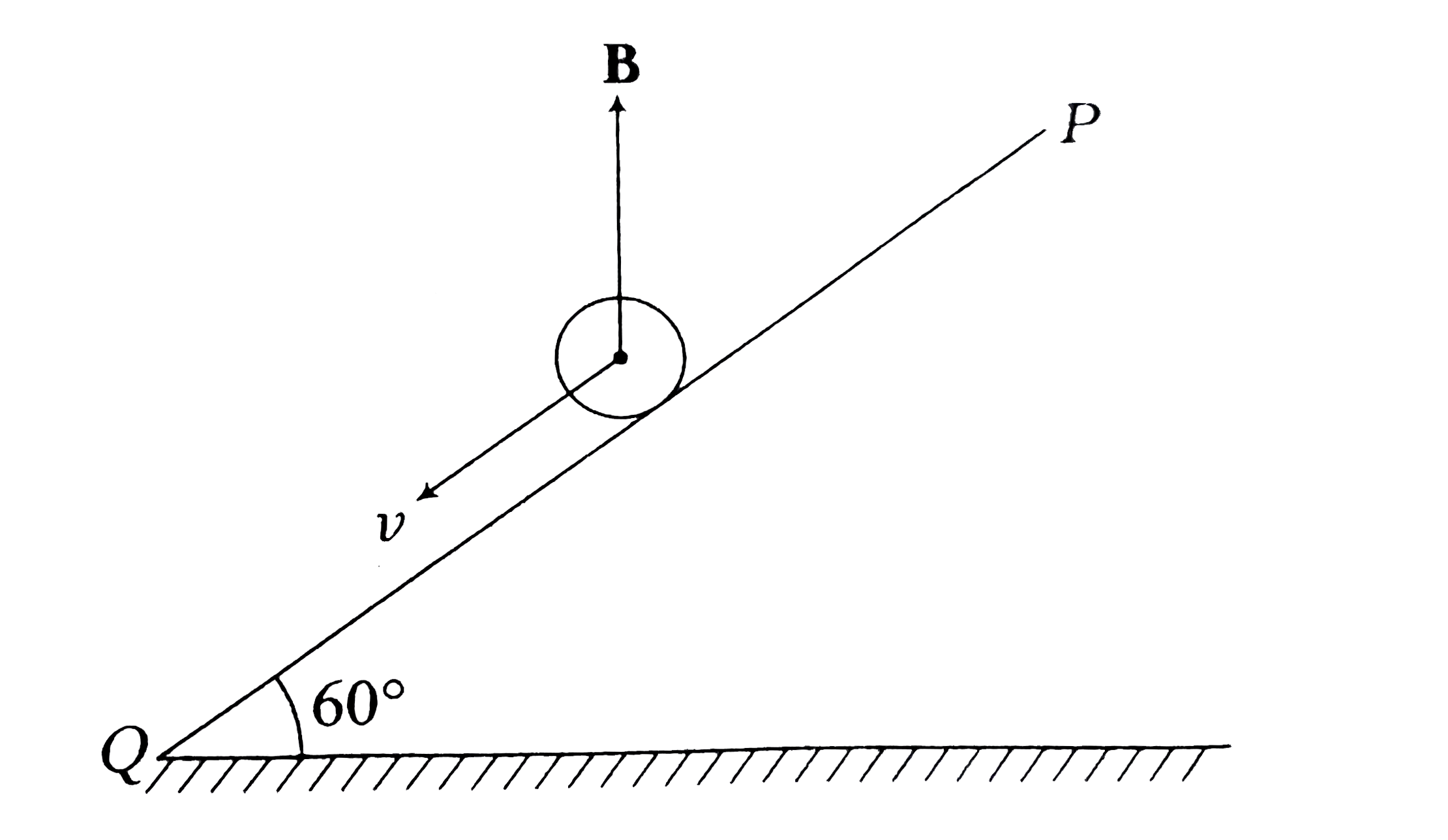
View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination θ with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field →B exists in space. Then, magnitude of magnetic field →B is

View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination θ with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field →B exists in space. Then, magnitude of magnetic field →B is

View SolutionTwo electrons move parallel to each other with equal speed 'V' the ratio of magnetic & electric force between them is
View SolutionTwo wedges, each of mass m, are placed next to each other on a flat horizontal floor. A cube of mass M is balanced on the wedges as shown in figure. Assume no friction between the cube and the wedges, but a coefficent of static friction μ<1 between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges ?
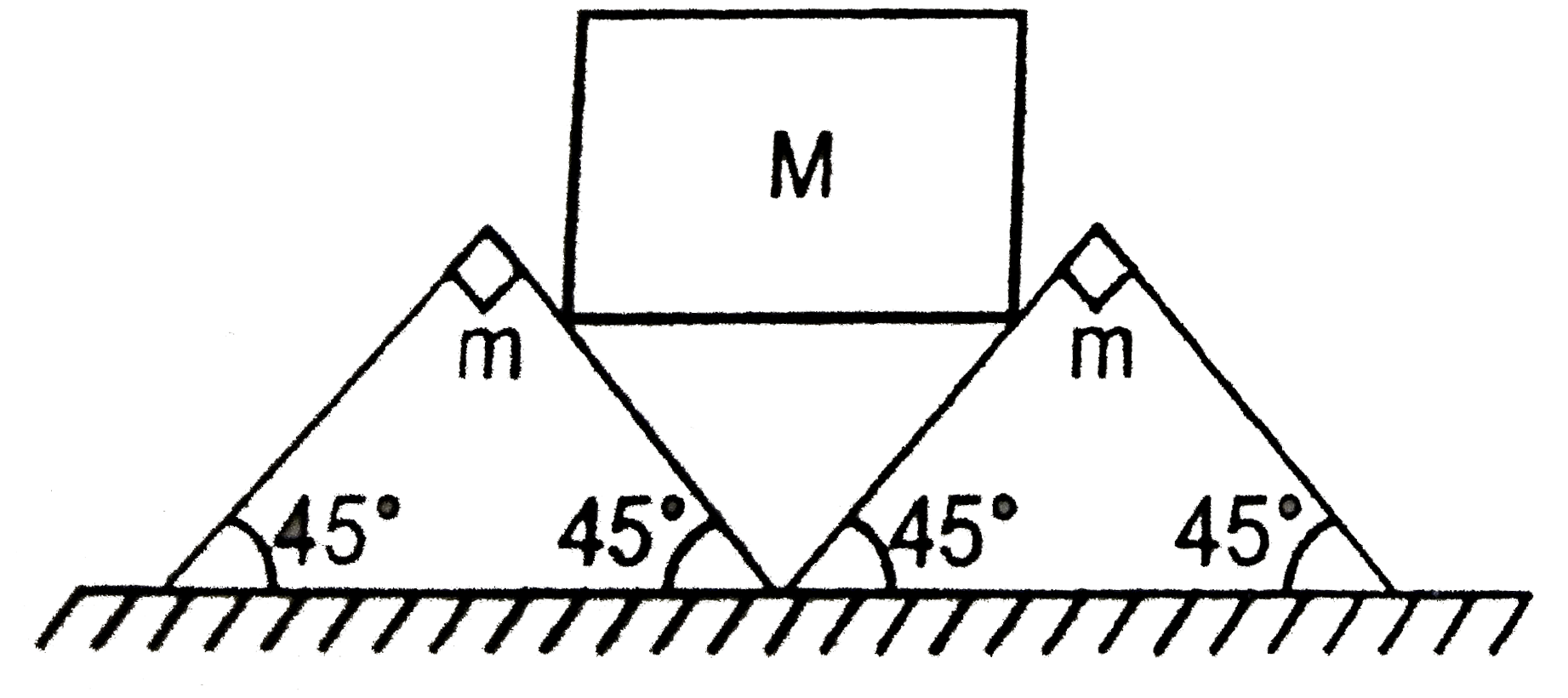
View SolutionA current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.

View SolutionTwo long wires a and b, carrying equal currents of 10*0A, are placed parallel to each other with a separation of 4*00 cm between them as shown in figure. Find the magnetic field B at each of the points P,Q and R.

View Solution
