The resistance of galvanometer is 999Ω. A shunt of 1Ω is connected to it. If the main current is 10−2A, what is the current flowing through the galvanometer.
To solve the problem, we need to find the current flowing through the galvanometer when a shunt is connected in parallel with it. Here’s a step-by-step solution:
Step 1: Identify the given values
- Resistance of the galvanometer, Rg=999Ω
- Resistance of the shunt, Rs=1Ω
- Main current, I=10−2A
Step 2: Calculate the equivalent resistance of the galvanometer and shunt in parallel
The formula for the equivalent resistance Req of two resistors in parallel is given by:
1Req=1Rg+1Rs
Substituting the values:
1Req=1999+11
1Req=1+999999=1000999
Thus,
Req=9991000Ω
Step 3: Use Ohm's law to find the voltage across the galvanometer and shunt
Using Ohm's law, V=I⋅R, we can find the voltage across the equivalent resistance when the main current flows through it:
V=I⋅Req=10−2⋅9991000
V=10−2⋅0.999=9.99×10−3V
Step 4: Calculate the current flowing through the galvanometer
Using Ohm's law again for the galvanometer:
Ig=VRg=9.99×10−3999
Calculating Ig:
Ig=10−2⋅999999=10−2⋅10−3=10−5A
Final Answer
The current flowing through the galvanometer is:
Ig=10−5A
---
- Resistance of the galvanometer, Rg=999Ω
- Resistance of the shunt, Rs=1Ω
- Main current, I=10−2A
The formula for the equivalent resistance Req of two resistors in parallel is given by:
1Req=1Rg+1Rs
Substituting the values:
1Req=1999+11
1Req=1+999999=1000999
Thus,
Req=9991000Ω
Using Ohm's law, V=I⋅R, we can find the voltage across the equivalent resistance when the main current flows through it:
V=I⋅Req=10−2⋅9991000
V=10−2⋅0.999=9.99×10−3V
Using Ohm's law again for the galvanometer:
Ig=VRg=9.99×10−3999
Calculating Ig:
Ig=10−2⋅999999=10−2⋅10−3=10−5A
The current flowing through the galvanometer is:
Ig=10−5A
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
Knowledge Check
If the galvanometer current is 10 mA, resistance of the galvanometer is 40Ω and shunt of 2Ω is connected to the galvanometer, the maximum current which can be measured by this ammeter is
A0.21AB2.1AC210AD21A
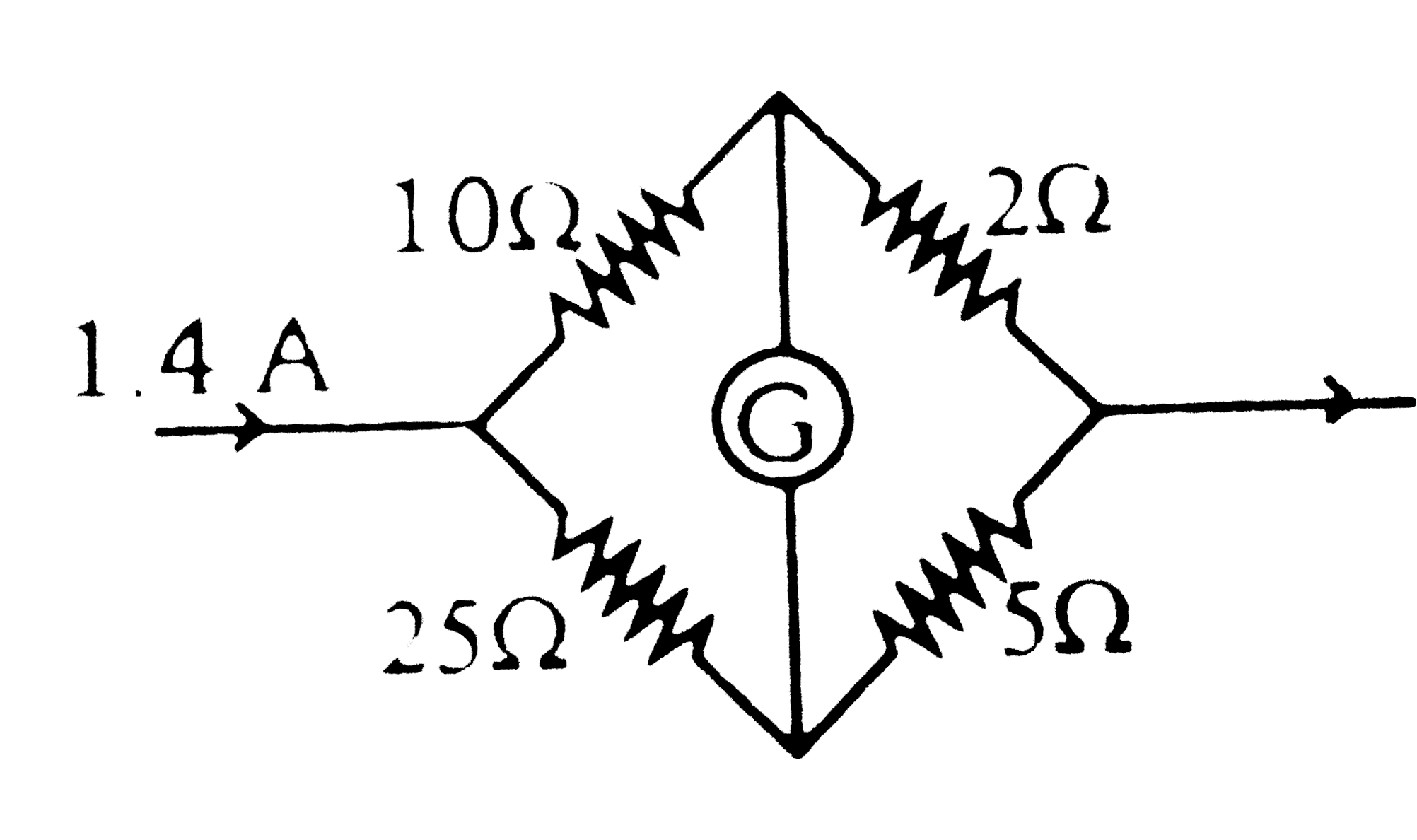
In the circuit, the current flowing through 10Ω resistance is
View SolutionA galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionIn a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
View SolutionWe have a galvanometer of resistance 25Ω. It is shunted by a 2.5Ω wire. The part of total current that flows through the galvanometer is given as
View SolutionA galvanometer has a resistance of 3663Ω. A shunt S is connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt is
View SolutionA galvanometer has a resistance of 3663Ω. A shunt S is connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt is
View SolutionA moving coil galvanometer has 50 turns and each turn has an area 210 . The magnetic field produced by the magnet inside the galvanometer is 0.02 . The torsional constant of the suspension wire is 10 . When a current flows through the galvanometer, a full scale deflection occurs if the coil rotates by 0.2 . The resistance of the coil of the galvanometer is 50 . This galvanometer is to be converted into an ammeter capable of measuring current in the range 01.0 . For this purpose, a shunt resistance is to be added in parallel to the galvanometer. The value of this shunt resistance, in , is __________.
View Solution