A cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vessel. Find the time taken by the vessel to become empty.
√2:1
1:√3
√3:1
1:1
The correct Answer is:A
Step by step video solution for A cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vessel. Find the time taken by the vessel to become empty. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA cylindrical vessel of area of cross-section A is filled with water to a height H. It has capillary tube of length l and radius r fitted horizontally at its bottom. If the coeffiecient of viscosity of water is η, then time required in which level will fall to a height H2 is (density of water is ρ)
View SolutionA cylindrical container of cross-section area, A is filled up with water upto height 'h' Water may exit through a tap of cross sectional area 'a' in the bottom of container. Find out

(a) Velocity of water just after opening of tap.
(b) The area of cross-section of water stream coming out of tape at depth h0 below tap in terms of 'a' just after opening of tap.
(c) Time in which conainer becomes empty.
(Given : (aA)1/2=0.22,h=20cm,h0=20cm
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the time required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
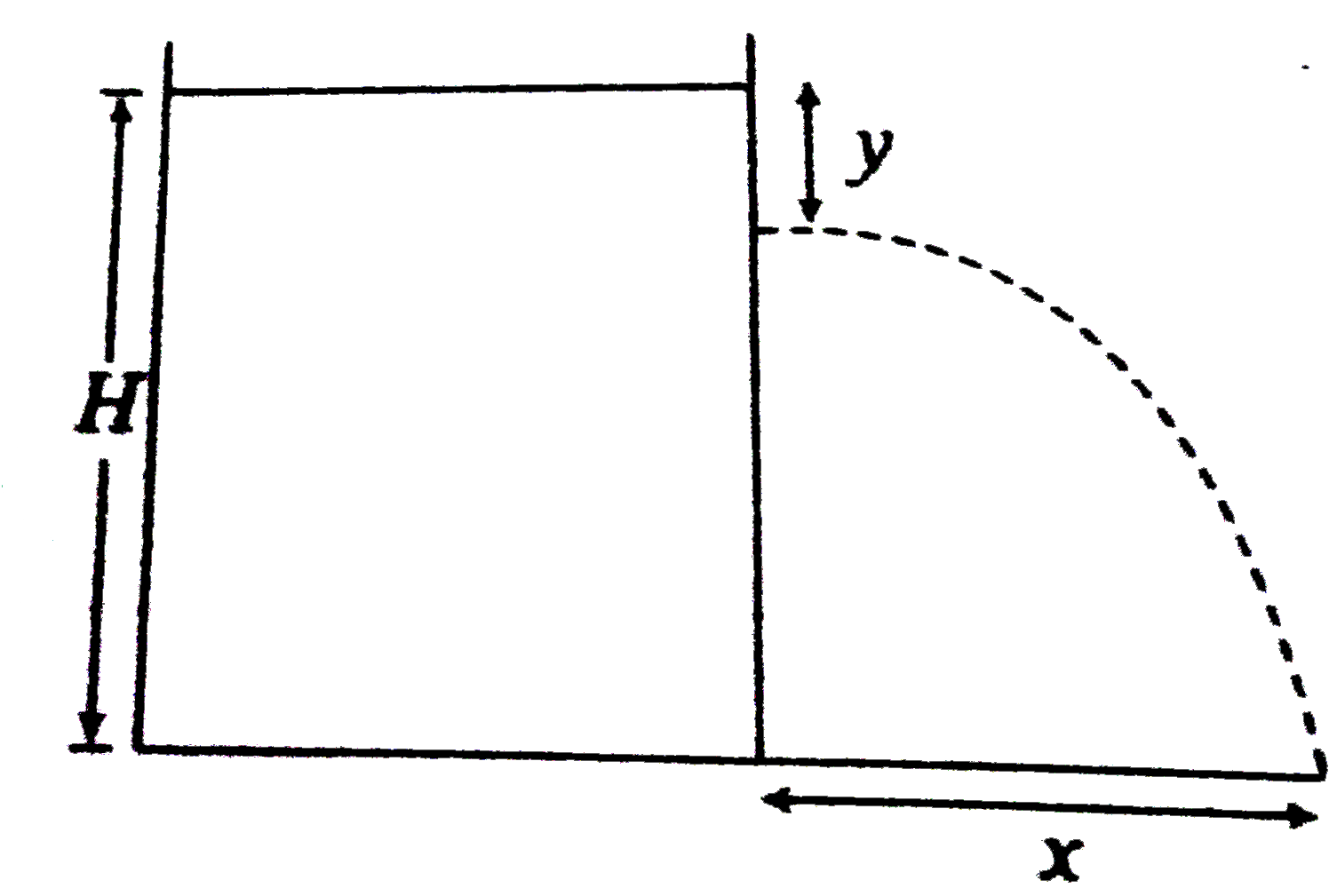
View SolutionA cylindrical vessel open at the top is 20cm high and 10cm in diameter. A circular hole of cross-sectional area 1cm2 is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate of 102cm3/s. The height of water in the vessel under steady state is (Take g=10m/s2).
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
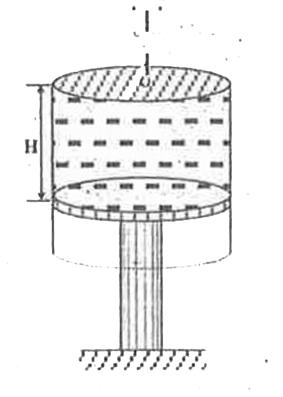
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is
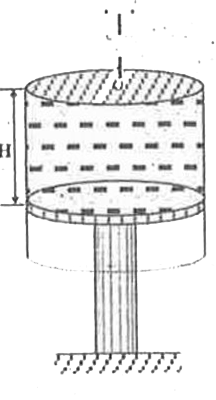
View Solution
