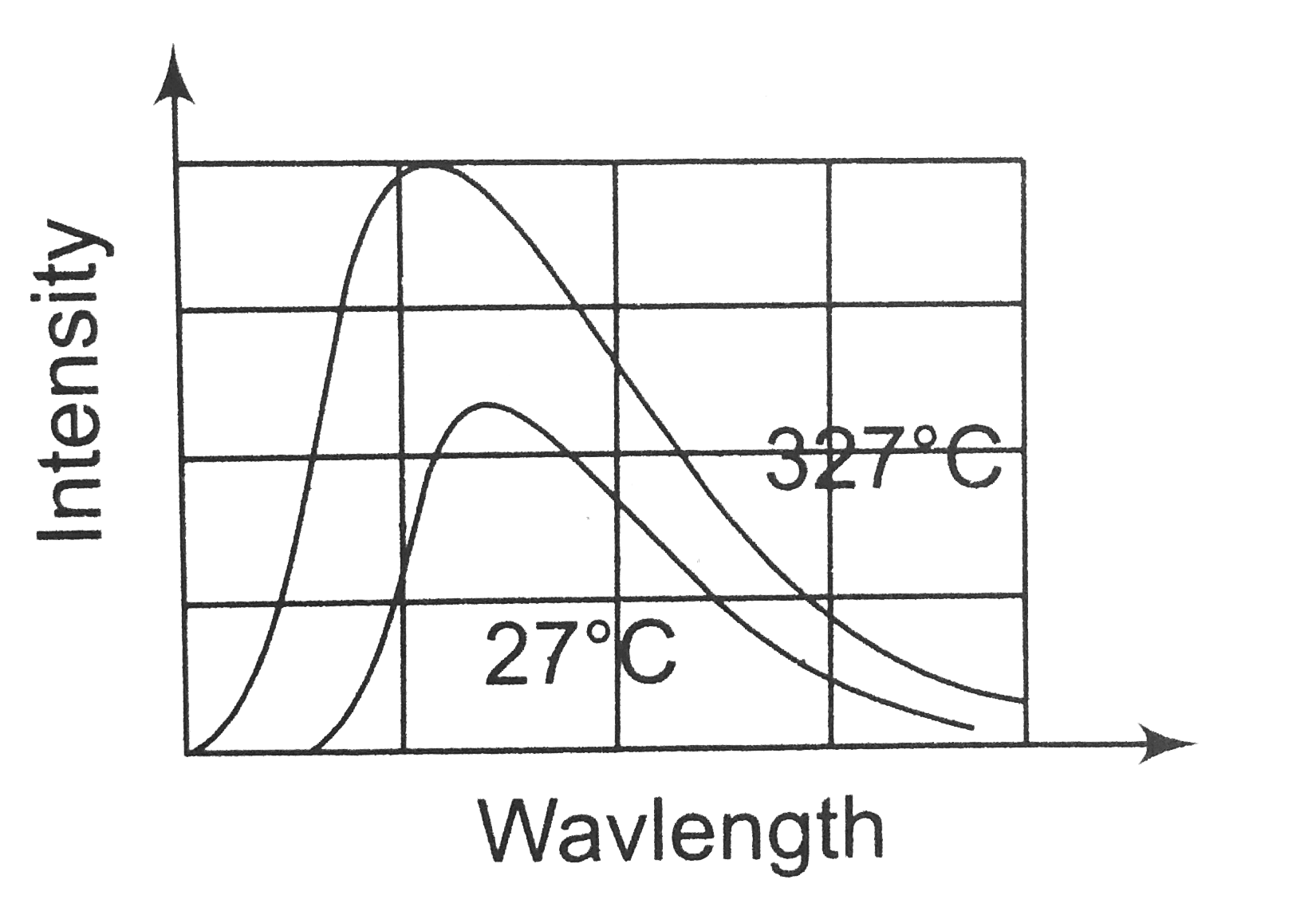
The spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1andA2 be the areas under the two curves respectively. The value of A2A1 is

1:16
4:1
2:1
16:1
The correct Answer is:D
Step by step video solution for The spectrum of a black body at two temperatures 27^(@)C and 327^(@)C is shown in the figure. Let A_(1) and A_(2) be the areas under the two curves respectively. The value of A_(2)/ A_(1) is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
 View Solution
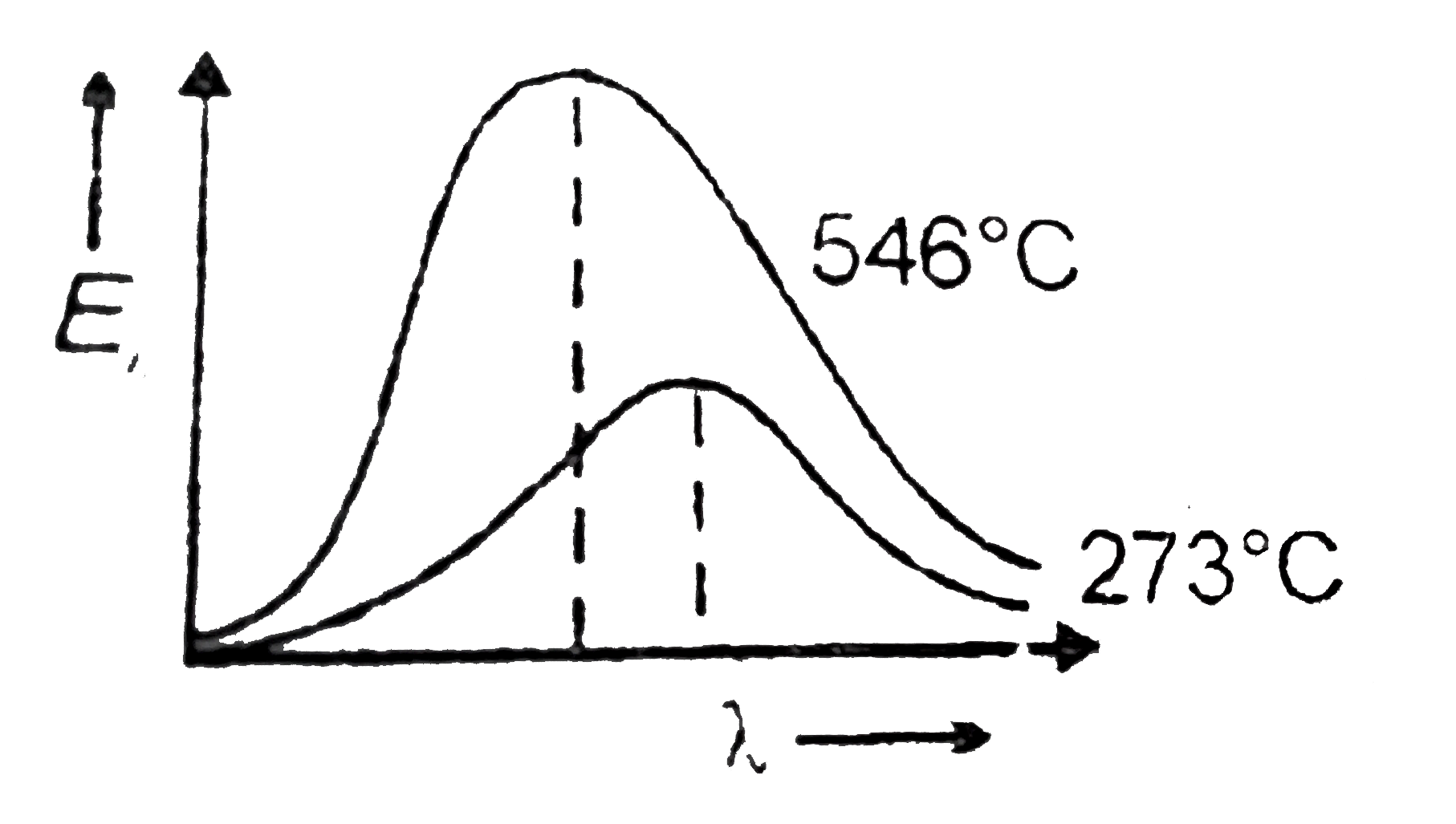
View SolutionThe spectra of a black body at temperatures 273∘C and 546∘C are shown in the figure. If A1 and A2 be area under the two curves respectively, the value of A2A1 is
 View Solution
View SolutionLet ABC and AB'C be two non-congruent triangles with sides BC=B'C=5, AC=6, and ∠A is fixed. If A1 and A2 are the area of the two triangles ABC and AB'C, then the value of A21+A22−2A1A2cos2A(A1+A2)2 is
View SolutionIf A1 and A2 be areas of two regular polygons having the same perimeter and number of sides be n and 2n respectively, then : A1A2 is
View SolutionA pulley-block arrangement is shown in the adjacent figure, if acceleration of m1,m2 and m3 are a1,a2 and a3 respectively, then relation between a1,a2 and a3 is ( All string and pulleys are ideal . )
 View Solution
View SolutionA1&A2 are two ores of metal M. Ar on calcination gives black precipitate, CO2& water.
 View Solution
View SolutionIf a1=2 and an−an−1=2n(n≥2), find the value of a1+a2+a3+…+a20.
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

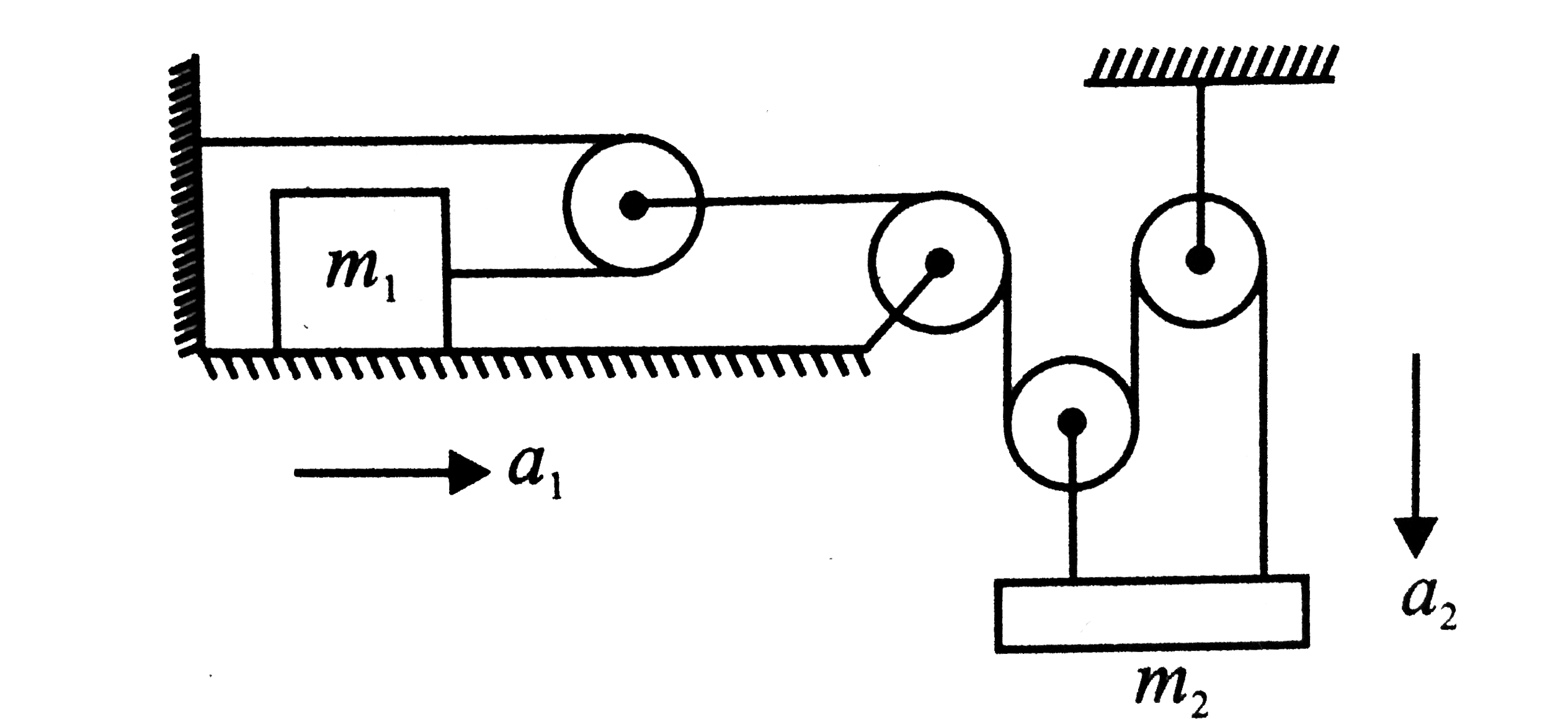
The value of acceleration a1 at the moment string RS is cut isView SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
 View Solution
View SolutionA1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
View Solution
