A block of mass m is attached to a spring of spring constant k is free to oscillate with angular velocity ω in a horizontal plane without friction or clamping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. the ammplitude of oscillationsin terms of ω,x0andv0 is
SHM along x-axis is x=Acos(ωt+φ0)
and velocity V=−Aωsin(ωt+φ0)
when t=0,x=x0 and v=v0
∴x0=acos(φ0)………1
and V0=−ωsinφ0 (or)
−V0ω=Asinφ0............2
Squaring and adding 1 and 2
x20+V20ω2=A2cos2φ0+A2sin2φ0
A2=x20+V20ω2 A=√x20+V20ω2
Similar Questions
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0.
View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View Solution
Knowledge Check
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0.
A√v20ω2−x20B√ω2v20+x20C√x20ω2+v20D√v20ω2+x20A particle of mass (m) is attached to a spring (of spring constant k) and has a natural angular frequency ω0. An external force R(t) proportional to cosωt(ω≠ω0) is applied to the oscillator. The time displacement of the oscillator will be proportional to.
Amω20−ω2B1m(ω20−ω2)C1m(ω20+ω2)Dmω20+ω2A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
Ax=0.05sin5t mBx=0.05cos5t mCx=0.5sin5t mDx=5sin5t m
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
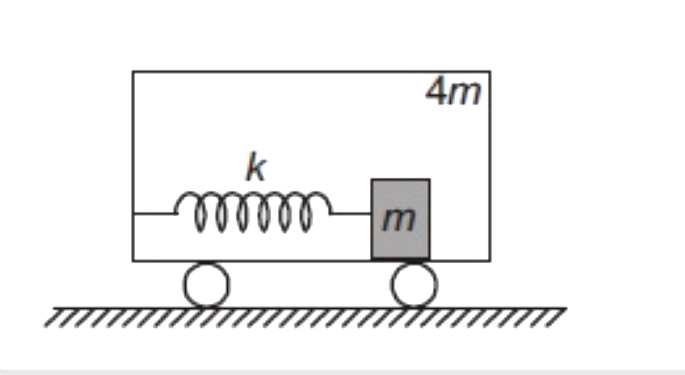
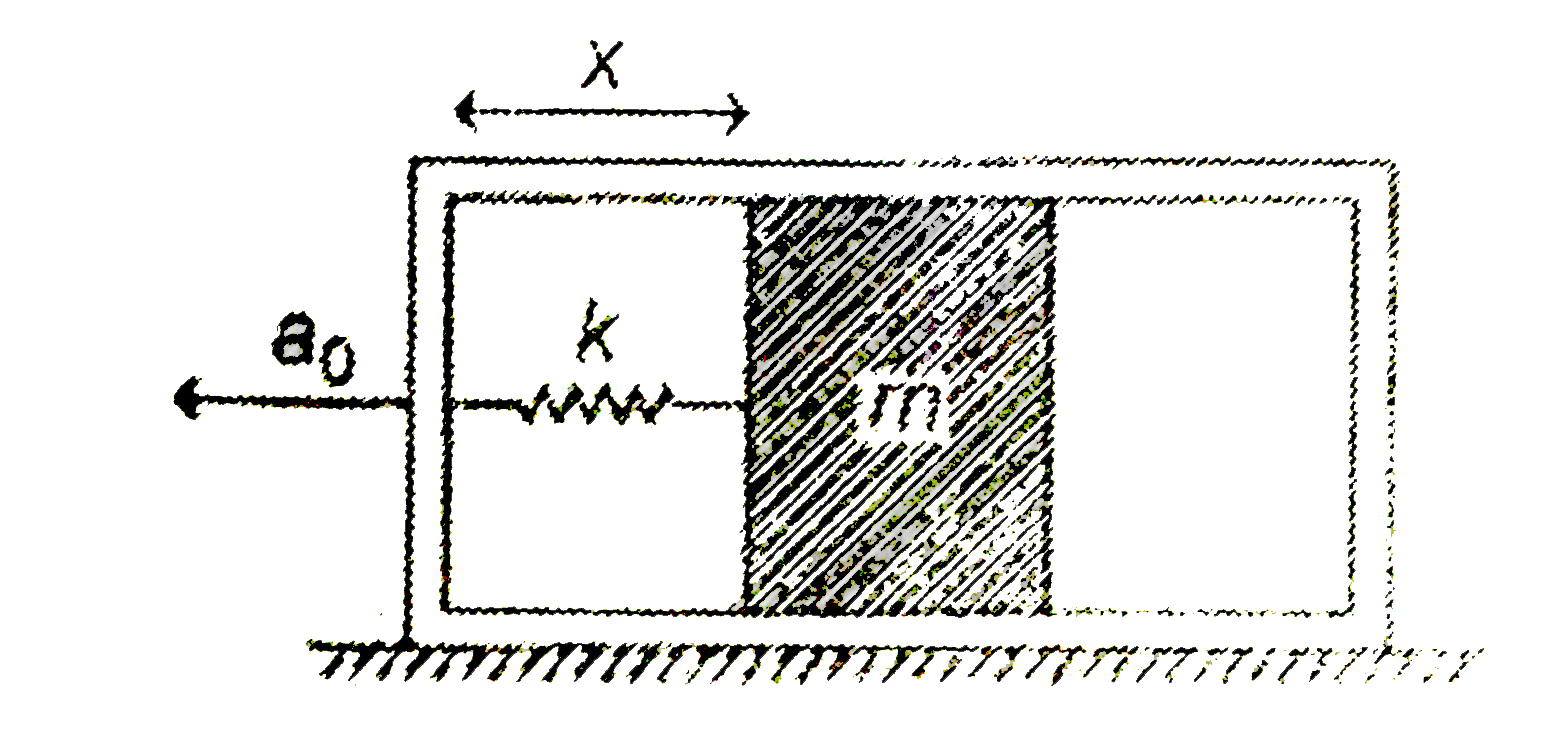
View SolutionA block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=x0+asinωt. An identical block B moving towards negative x -axis with velocity v0 collides elastically with block A at time t=0. Then
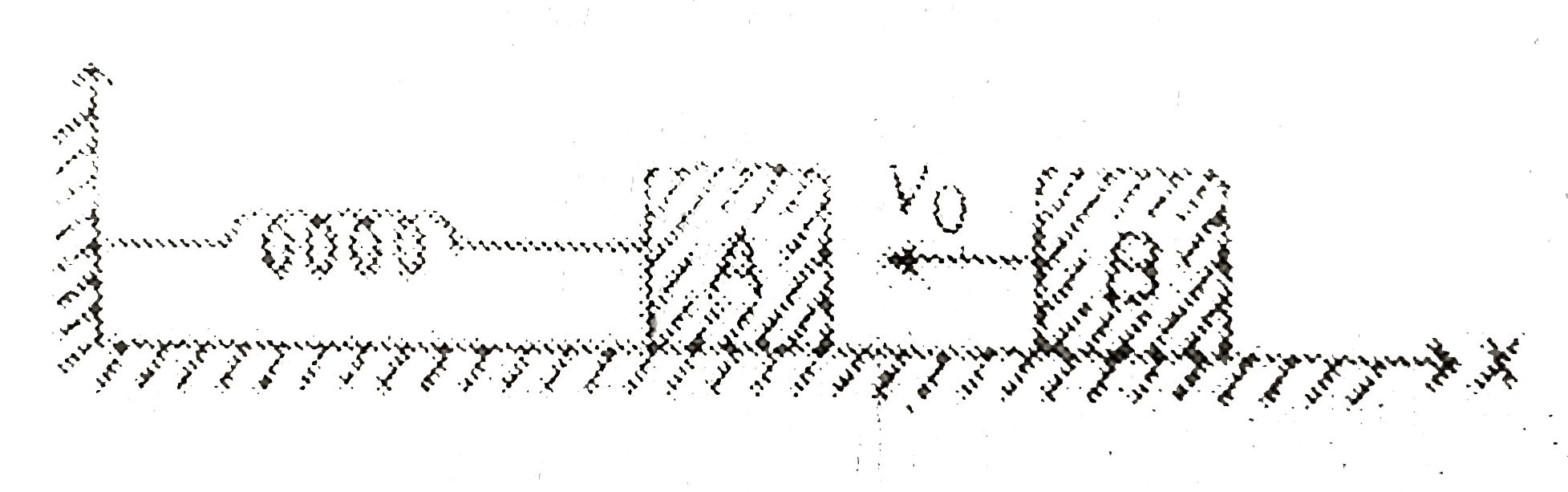
View Solution
