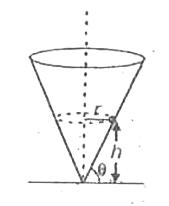
A particle describes a horizontal circle on the smooth surface of an inverted cone, the height of the plane of the circle above the vertex is 9.8 cm. Find the speed of the particle (g= 9.8m/s2) [See Fig.] (a) given in the answer section]
0.49ms−1
0.98ms−1
1.96ms−1
3.92ms−1
The correct Answer is:B
Step by step video solution for A particle describes a horizontal circle on the smooth surface of an inverted cone, the height of the plane of the circle above the vertex is 9.8 cm. Find the speed of the particle (g= 9.8 m//s^2) [See Fig.] (a) given in the answer section] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
View SolutionA particle describes a horizontal circle in a conical funne whoses inner surface is smooth with speed of 0.5m/s . What is the height of the plane of circle from vertex the funnel?
View SolutionA particle describes a horizontal circle in a conical funne whoses inner surface is smooth with speed of 0.5m/s . What is the height of the plane of circle from vertex the funnel?
View SolutionA particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The heigh of the plane of motion above the vertex is hh and the semi-vertical angle of the cone is α The period of revolution of the particle

View SolutionThe area of the curved surface of a cone is 60π cm2. If the slant height of the cone be 8cm, find the radius of the base.
View SolutionA particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is θ, then
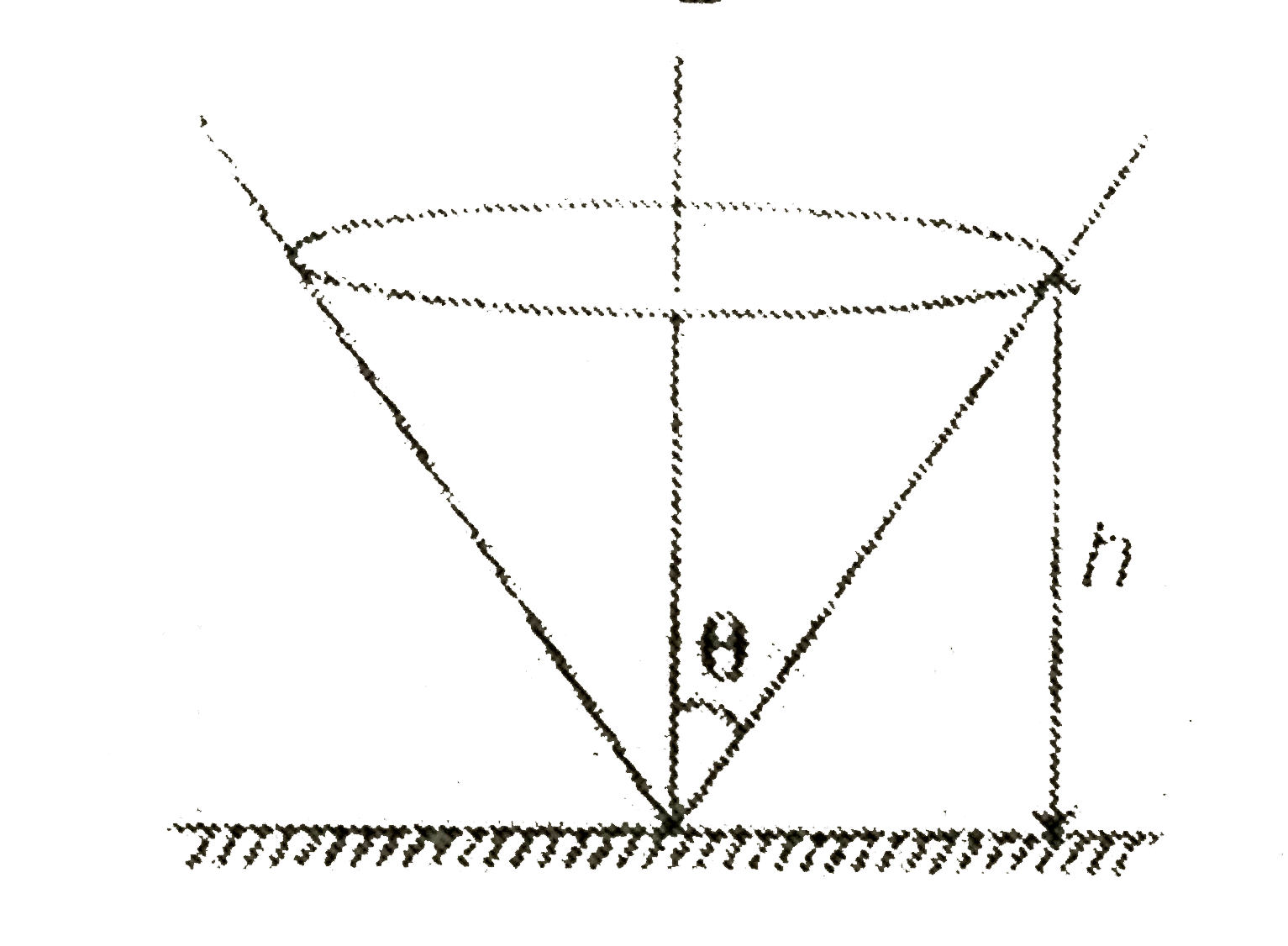
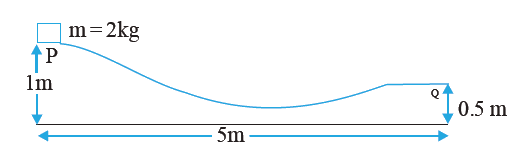
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
View SolutionWhat is the value of g at a height 8848 m above sea level. Given g on the surface of the earth is 9.8ms−2. Mean radius of the earth =6.37×106m.
View SolutionA particle is launched from a height 8R above the surface of earth and it is given a speed (GM8R) parallel to the surfaces then
View SolutionFind the value of 'g(i)' at a height of 100 km (ii) at height 6400 km from the surface of the earth. (Radius of the earth = 6400 km, g on the surface of the earth =9.8ms−2.
View Solution
