The distance between two moving particles at any time is α. If v be their relative velocity and v1 and v2 be the component of v along and perpendicular to a. The time when they are closest to each other are
a(v+vr)v,a(1+vru)2
av(v+vr),a(1+uvr)2
avrv,avru2
avvr,auv2r
The correct Answer is:D
Step by step video solution for The distance between two moving particles at any time is alpha. If v be their relative velocity and v_(1) and v_(2) be the component of v along and perpendicular to a. The time when they are closest to each other are by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The distance between two moving particles P and Q at any time is a.If vr be their relative velocity and if u and v be the components of vr, along and perpendicular to PQ.The closest distance between P and Q and time that elapses before they arrive at their nearest distance is
View SolutionThe displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
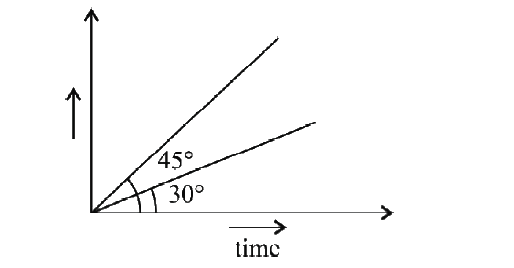
View SolutionThe displacement time graph of two moving particles make angles of 30∘ and 45∘ with the x-axis. The ratio of the two velocities VAandVB is
View SolutionA particle is moving with velocity v=100ms−1. If one of the rectangular components of a velocity is 50ms−1. Find the other component of velocity and its angle with the given component of velocity.
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v1=1 ms−1 and v2=4 ms−1 horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
View SolutionA man traversed half the distance with a velocity v0. The remaining part of the distance was covered with velocity v1. For half the time and with velocity v2 for the other half of the time . Find the average speed of the man over the whole time of motion.
 .
.
View SolutionAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View Solution
