With usual notation, the time period of rotation of a satellite orbiting close to the surface of earth
(a) ,(b)84.6 minutes ,(c) , (d)
a is only correct
a & b are correct
a,b & c are correct
a,b & d are correct
The correct Answer is:C
To find the time period of rotation of a satellite orbiting close to the surface of the Earth, we can derive the formula step by step.
Step 1: Understand the parameters
- Let R be the radius of the Earth.
- Let g be the acceleration due to gravity at the surface of the Earth.
- The satellite is orbiting at a distance r from the center of the Earth, which is approximately equal to R when it is close to the surface.
Step 2: Use the formula for orbital velocity
The orbital velocity v of a satellite is given by the formula:
v=√GMr
where G is the gravitational constant and M is the mass of the Earth. When the satellite is very close to the Earth's surface, we can approximate r as R:
v=√GMR
Step 3: Relate velocity to the time period
The time period T of the satellite's orbit is related to the orbital velocity and the circumference of the orbit:
T=2πrv
Substituting r with R and the expression for v:
T=2πR√GMR
Step 4: Simplify the expression
Rearranging the equation gives:
T=2πR⋅√RGM=2π√R3GM
Step 5: Use the relationship between g, G, and M
We know that the acceleration due to gravity g can be expressed as:
g=GMR2
From this, we can express GM as:
GM=gR2
Substituting this back into the time period formula gives:
T=2π√R3gR2=2π√Rg
Step 6: Calculate the time period
Using the known values:
- R≈6.4×106m
- g≈9.8m/s2
Substituting these values into the formula:
T=2π√6.4×1069.8
Calculating this will yield a time period of approximately 84.6 minutes.
Conclusion
Thus, the correct option for the time period of rotation of a satellite orbiting close to the surface of the Earth is:
(b) 84.6 minutes.
---
- Let R be the radius of the Earth.
- Let g be the acceleration due to gravity at the surface of the Earth.
- The satellite is orbiting at a distance r from the center of the Earth, which is approximately equal to R when it is close to the surface.
The orbital velocity v of a satellite is given by the formula:
v=√GMr
where G is the gravitational constant and M is the mass of the Earth. When the satellite is very close to the Earth's surface, we can approximate r as R:
v=√GMR
The time period T of the satellite's orbit is related to the orbital velocity and the circumference of the orbit:
T=2πrv
Substituting r with R and the expression for v:
T=2πR√GMR
Rearranging the equation gives:
T=2πR⋅√RGM=2π√R3GM
We know that the acceleration due to gravity g can be expressed as:
g=GMR2
From this, we can express GM as:
GM=gR2
Substituting this back into the time period formula gives:
T=2π√R3gR2=2π√Rg
Using the known values:
- R≈6.4×106m
- g≈9.8m/s2
T=2π√6.4×1069.8
Calculating this will yield a time period of approximately 84.6 minutes.
Thus, the correct option for the time period of rotation of a satellite orbiting close to the surface of the Earth is:
(b) 84.6 minutes.
Similar Questions
If T1 and T2 are the time-periods of oscillation of a simple pendulum on the surface of earth (of radius R) and at a depth d, the d is equal to
View SolutionThe period of revolution of a satellite in an orbit of radius 2R is T. What will be its period of revolution in an orbit of radius 8R ?
View Solution
Knowledge Check
A geo-stationary satellite orbits around the earth in a circular orbit of radius 36000 km. Then, the time period of a spy satellite orbiting a few hundred kilometers above the earth's surface (R_("Earth") = 6400 " km") will approximately be
A1/2 hrB1 hrC2 hrD4 hrImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to R−5/2, then
(a) T2 is proportional to R2
(b) T2 is proportional to R7/2
(c) T2 is proportional to R3/3
(d) T2 is proportional to R3.75.AR3/2BR3/5CR7/2DR7/2
A simple pendulum suspended from the ceilling of a stationary trolley has a length l. its period of oscillation is 2π√l/g. What will be its period of oscillation if the trolley moves forward with an acceleration f ?
A. 2π√lf−g
B. 2π√lf+g
C. 2π√l(f2+g2)1/2
D. 2π√lf2−g2
View SolutionWhat is the mass of the planet that has a satellite whose time period is T and orbital radius is r?
View Solution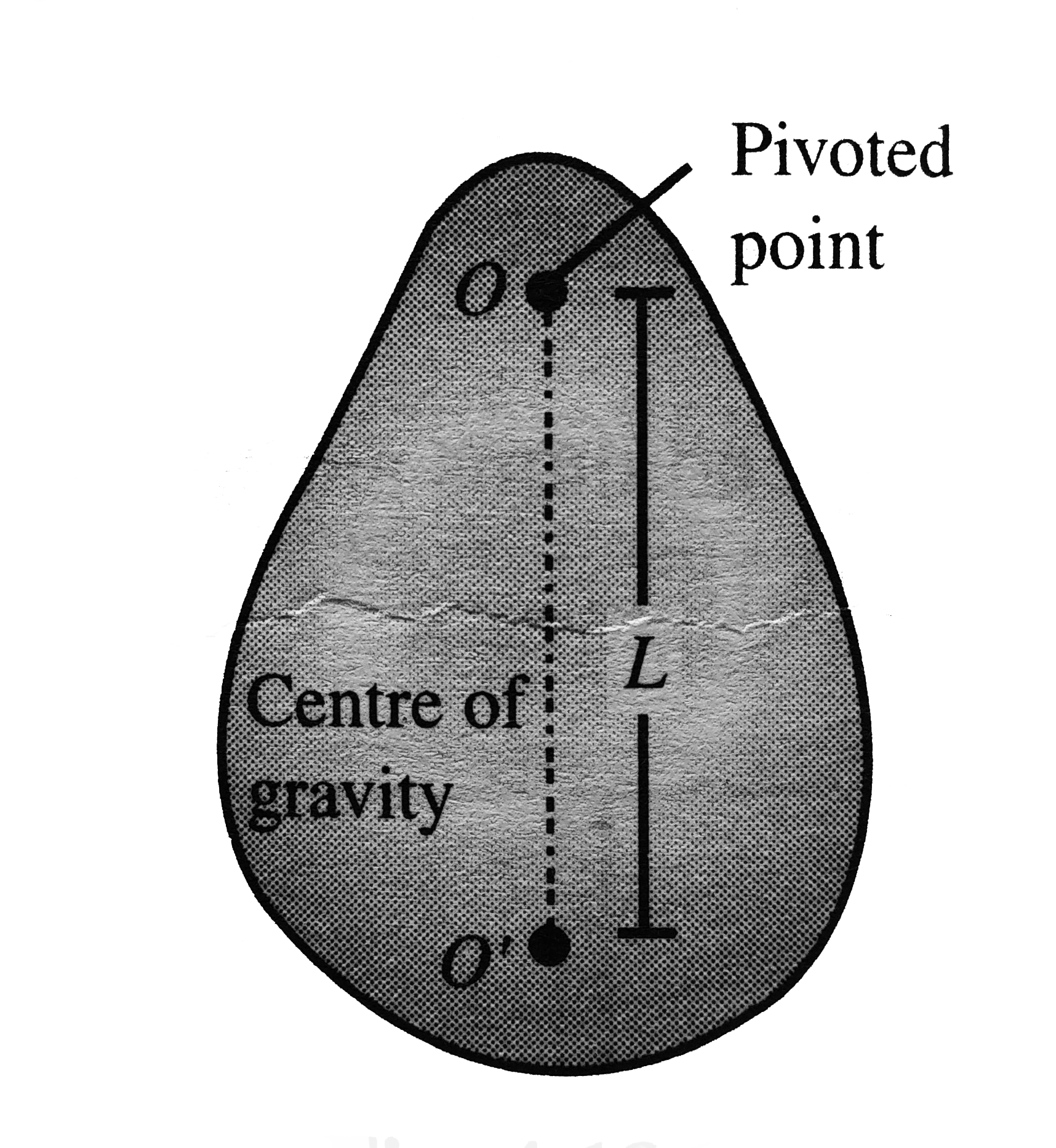
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.
View SolutionIf T=2π√18, then relative errors in T and l are in the ratio
View SolutionA satellite having time period same as that of the earth's rotation about its own axis is orbiting the earth at a height 8R above the surface of earth. Where R is radius of earth. What will be the time period of another satellite at a height 3.5 R from the surface of earth ?
View SolutionIt is known that the time of revolution T of a satellite around the earth depends on the universal gravitational constant G, the mass of the earth M, and the radius of the circular orbit R. Obtain an expression for T using dimensional analysis.
View Solution
