Question

Find the potential energy of a system of four particles placed at the vertices of a square of side l. Also obtain the potential at the centre of the square.

Explanation

To find the potential energy of a system of four particles placed at the vertices of a square of side length $$l$$, we can follow these steps:

Step 1: Understand the Configuration
We have four particles (charges) located at the vertices of a square. Let's denote the charges as \( q \) at each vertex.

Step 2: Calculate the Work Done in Bringing the Charges
The potential energy of the system can be calculated by determining the work done to bring each charge from infinity to its position at the vertices of the square.

1. Bringing the First Charge:
- The work done \( W_1 \) to bring the first charge \( q \) from infinity to a vertex is zero since there are no other charges present.
\( W_1 = 0 \)

2. Bringing the Second Charge:
- The work done \( W_2 \) to bring the second charge \( q \) to a vertex (while the first charge is already there) is given by the formula:
\( W_2 = k \frac{q^2}{l} \)
where \( k \) is Coulomb's constant.

3. Bringing the Third Charge:
- The work done \( W_3 \) to bring the third charge \( q \) to a vertex (with two charges already present) involves two interactions:
\( W_3 = k \frac{q^2}{l} + k \frac{q^2}{\sqrt{2}l} = k \frac{q^2}{l} + k \frac{q^2}{2l} = k \frac{3q^2}{2l} \)

4. Bringing the Fourth Charge:
- The work done \( W_4 \) to bring the fourth charge \( q \) to a vertex (with three charges already present) involves three interactions:
\( W_4 = k \frac{q^2}{l} + k \frac{q^2}{l} + k \frac{q^2}{\sqrt{2}l} = 2k \frac{q^2}{l} + k \frac{q^2}{\sqrt{2}l} = k \left(2 + \frac{1}{\sqrt{2}}\right) \frac{q^2}{l} \)

Step 3: Calculate Total Work Done
Now, we can sum up all the work done to find the total potential energy \( U \) of the system:
\( U = W_1 + W_2 + W_3 + W_4 = 0 + k \frac{q^2}{l} + k \frac{3q^2}{2l} + k \left(2 + \frac{1}{\sqrt{2}}\right) \frac{q^2}{l} \)
This simplifies to:
\( U = k \left(1 + \frac{3}{2} + 2 + \frac{1}{\sqrt{2}}\right) \frac{q^2}{l} \)
Calculating the coefficients gives:
\( U = k \left(\frac{7}{2} + \frac{1}{\sqrt{2}}\right) \frac{q^2}{l} \)

Step 4: Calculate the Potential at the Center of the Square
To find the potential \( V \) at the center of the square, we consider the contributions from all four charges:
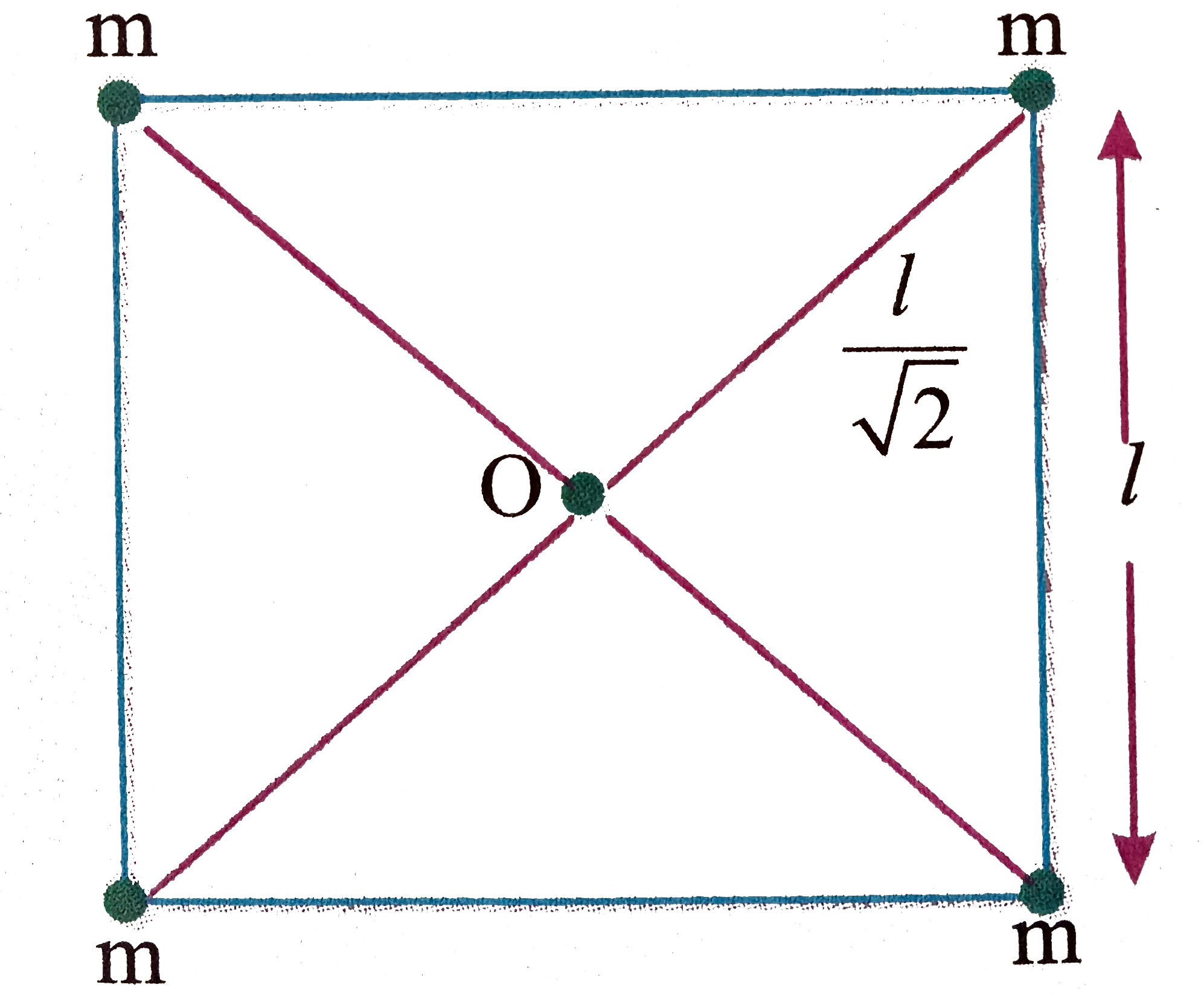
- The distance from each vertex to the center of the square is \( \frac{l}{\sqrt{2}} \).
- The potential at the center due to one charge \( q \) is:
\( V = k \frac{q}{\frac{l}{\sqrt{2}}} = k \frac{q \sqrt{2}}{l} \)
Thus, the total potential at the center due to all four charges is:
\( V_{total} = 4 \cdot k \frac{q \sqrt{2}}{l} = \frac{4kq\sqrt{2}}{l} \)

Final Answers
- The potential energy of the system is:
\( U = k \left(\frac{7}{2} + \frac{1}{\sqrt{2}}\right) \frac{q^2}{l} \)
- The potential at the center of the square is:
\( V_{total} = \frac{4kq\sqrt{2}}{l} \)