A vertical glass capillary tube open at both ends contain some water (T.P). Then the length of water column L = _____
To solve the problem of finding the length of the water column L in a vertical glass capillary tube open at both ends, we can follow these steps:
1. Understanding the Setup:
- We have a vertical glass capillary tube that is open at both ends and contains water.
- The pressure at different points in the tube will vary due to the effects of surface tension.
2. Identify the Pressures:
- Let P0 be the atmospheric pressure outside the tube.
- The pressure at the top of the water column (let's call it P2) can be expressed as:
P2=P0−2TR
where T is the surface tension of the water and R is the radius of the capillary tube.
3. Pressure at the Bottom of the Water Column:
- The pressure at the bottom of the water column (let's call it P3) can be expressed using hydrostatic pressure:
P3=P2+ρgL
where ρ is the density of water, g is the acceleration due to gravity, and L is the length of the water column.
4. Equating Pressures:
- The pressure at the bottom of the water column can also be expressed as:
P3=P0
- Therefore, we can set the two expressions for P3 equal to each other:
P0=P2+ρgL
5. Substituting for P2:
- Substitute the expression for P2 into the equation:
P0=(P0−2TR)+ρgL
6. Rearranging the Equation:
- Rearranging gives:
2TR=ρgL
7. Solving for Length L:
- Finally, we can solve for L:
L=2TρgR
Final Answer:
The length of the water column L in the capillary tube is given by:
L=2TρgR
- We have a vertical glass capillary tube that is open at both ends and contains water.
- The pressure at different points in the tube will vary due to the effects of surface tension.
- Let P0 be the atmospheric pressure outside the tube.
- The pressure at the top of the water column (let's call it P2) can be expressed as:
P2=P0−2TR
where T is the surface tension of the water and R is the radius of the capillary tube.
- The pressure at the bottom of the water column (let's call it P3) can be expressed using hydrostatic pressure:
P3=P2+ρgL
where ρ is the density of water, g is the acceleration due to gravity, and L is the length of the water column.
- The pressure at the bottom of the water column can also be expressed as:
P3=P0
- Therefore, we can set the two expressions for P3 equal to each other:
P0=P2+ρgL
- Substitute the expression for P2 into the equation:
P0=(P0−2TR)+ρgL
- Rearranging gives:
2TR=ρgL
- Finally, we can solve for L:
L=2TρgR
The length of the water column L in the capillary tube is given by:
L=2TρgR
Similar Questions
A vertical glass capillary tube, open at both ends, contains some water. Which of the following shapes may not be taken by the water -in the tube?
View SolutionA long horizontal glass capillary tube open at both ends contains a mercury thread 1 m long at 0∘C. Find the length of the mercury thread, as read on this scale, at 100∘C.
View SolutionWater rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45∘, the length of water risen in the tube will be
View SolutionA horizontal tube, open at both ends, contains a column of liquid. The length of this liquid column does not change with temperature. Let γ : coefficient of volume expansion of the liquid and α : coefficient of linear expansion of the material of the tube
View SolutionA vertical capillary tube with inside radius 0.25 mm is submerged into water so that the length of its part protruding over the water surface is equal to 25 mm . Surface tension of water is 73×10−3 N/m and angle of contact is zero degree for glass and water , acceleration due to gravity 9.8 m/s^2. Then choose correct statement .
where R is radius of menisus and h is height of water in capillary tube .
View Solution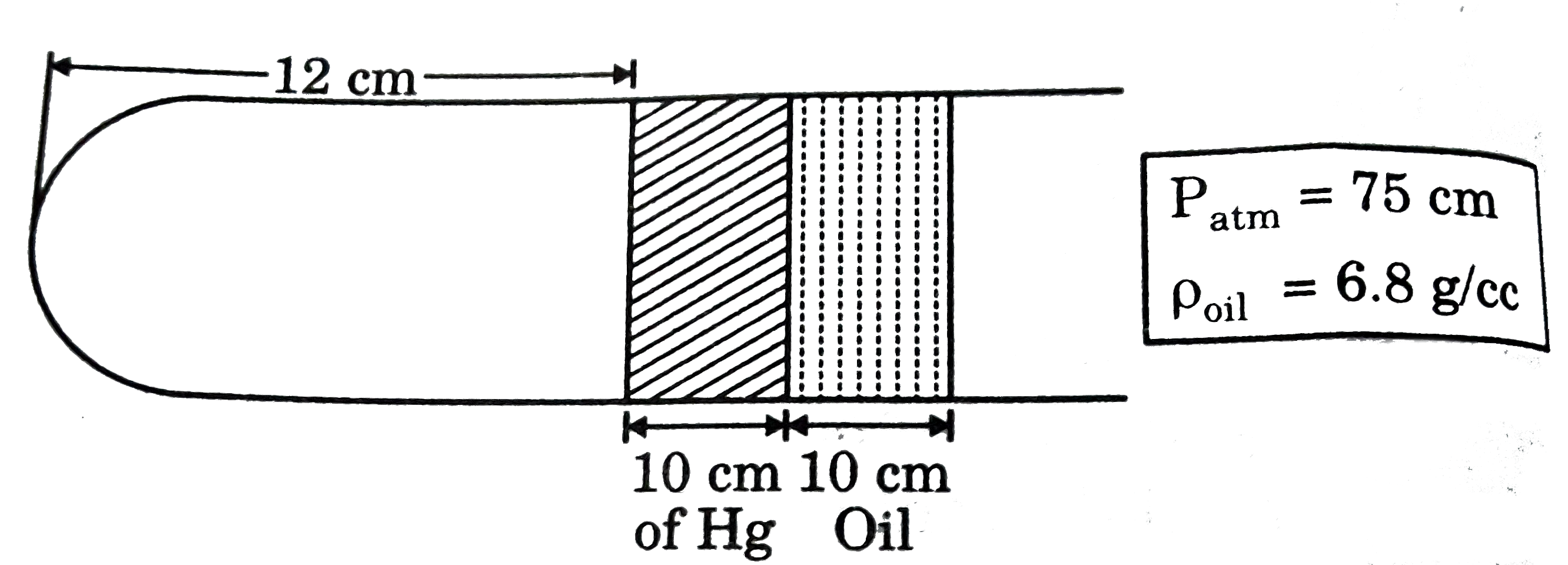
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionA capillary tube of radius 0.20 mm is dipped vertically in water. Find the height of the water column raised in the tube. Surface tension of water =0.075Nm−1 and density of water =1000kgm−3.Takeg=10ms−2.
View SolutionIn a capillary tube experiment, a vertical 30 cm long capillary tube is dipped in water. The water rises up to a height of 10 cm due to capillary action. If this experiment is conducted in a freely falling elevator, the length of te water column becomes
View SolutionA U-shaped tube open to the air at both ends contains some mercury. A quantity of water is carefully poured into the left arm of the U-shaped tube until the vertical height of the water column is 15.0cm.
(a) What is the gauge pressure at the water mercury interface ?
(b) Calculate the vertical distance h from the top of the mercury in the right hand arm of the tube to the top of the water in the left-hand arm.
 .
.
View SolutionA 10.0 cm column of air is trapped by a column of Hg 4.00 cm long in capillary tube of uniform bore when the tube is held horizontally in a room at 1 atm. Length of the air column when the tube is held vertically with the open end up is

View Solution
