A lead shot of 1nm diameter falls through a long column of glycerine. The variation of its velocity v with distance covered is represented by
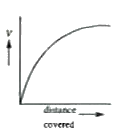

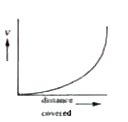
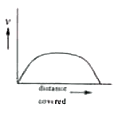
The correct Answer is:A
Step by step video solution for A lead shot of 1nm diameter falls through a long column of glycerine. The variation of its velocity v with distance covered is represented by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A lead shot of 1 mm diameter falls through a long colummn of glycerine. The variation of the velocity v with distance covered (s) is represented by
View SolutionFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionA bar magnet is made to fall through a long vertica! copper tube. The speed (V) of the magnet as a function of time (t) is best represented by

View SolutionTwo identical source moving parallel to each other at seperation 'd' are producing sounds of frequency 'f' and are moving with constant velocity v0. A stationary .observer 'O' is on the line of motion of one of the sources. Then the variation of beat frequency heard by O with time is best represented by: (as they come from large distance and go to a large distance)
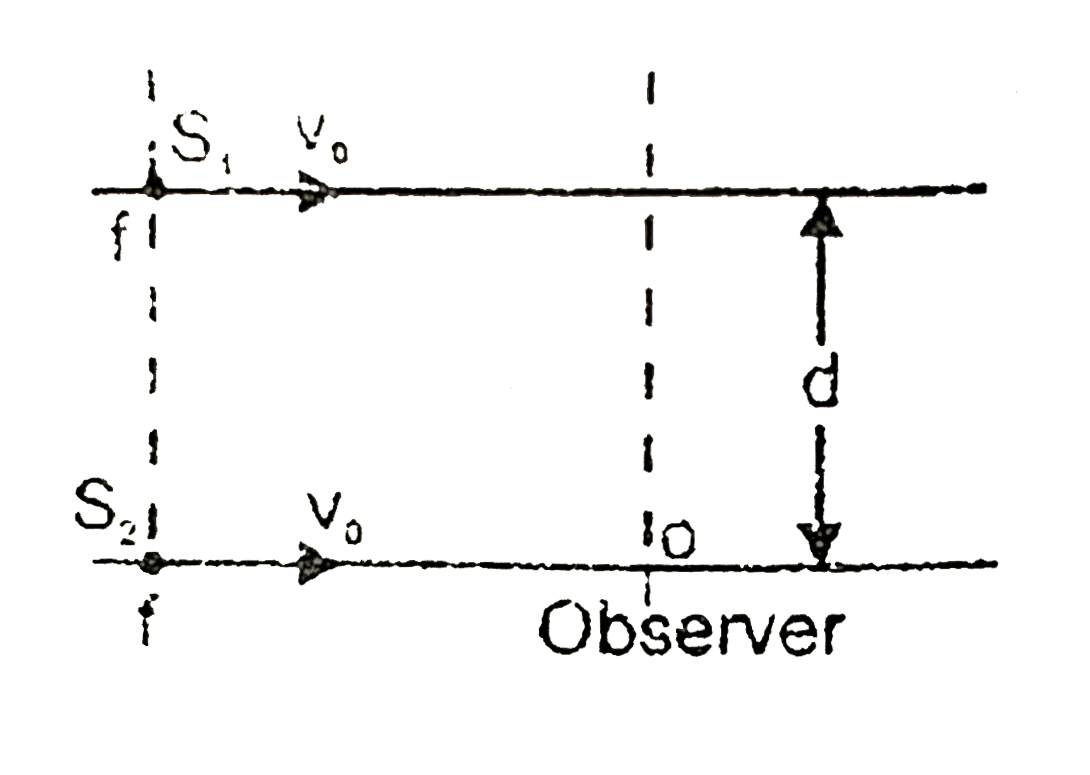
View SolutionTwo ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by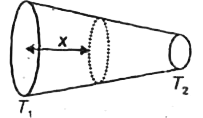
View SolutionAt freezing point of a solution there is always
View SolutionA spherical steel ball released at the top of along column of glycerin of length l falls through a distance l/2 with accelerated motion and the remaining distance l/2 with uniform velocity let t1 and t2 denote the times taken to cover the first and second half and w1 and w2 are the work done against gravity in the two halves, then compare times and work done.
View SolutionA point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = K√S where 'K' is a constant. If ' theta' is the angle between the total acceleration and tangential acceleration, then
View SolutionA charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).

View Solution
