A wheel having metal spokes of 1m long between its axle and rim is rotating in a magnetic field of flux density 5×10−5T normal to the plane of the wheel. An e.m.f of 22/7 mV is produced between the rim and the axle of the wheel. The rate of rotation of the wheel in revolutions per seconds is
10
20
30
4
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the given data
We are given:
- Length of the spokes (r) = 1 m
- Magnetic flux density (B) = 5×10−5T
- E.M.F (E) = 227mV=227×10−3V
Step 2: Write down the formula for E.M.F
The formula for the induced E.M.F in a rotating wheel is given by:
E=12Bωr2
where:
- E is the induced E.M.F,
- B is the magnetic flux density,
- ω is the angular velocity in radians per second,
- r is the radius (length of the spokes).
Step 3: Rearrange the formula to find ω
Rearranging the formula to solve for ω:
ω=2EBr2
Step 4: Substitute the known values into the equation
Substituting the values into the equation:
ω=2×(227×10−3)5×10−5×(1)2
Step 5: Calculate ω
Calculating the numerator:
2×(227×10−3)=447×10−3
Calculating the denominator:
5×10−5×12=5×10−5
Now substituting these into the equation:
ω=447×10−35×10−5=44×10−37×5×10−5=44×10−335×10−5=4435×102=1.2571×102rad/s
Thus,
ω≈125.71rad/s
Step 6: Convert angular velocity to revolutions per second
We know that:
ω=2πn
where n is the number of revolutions per second. Rearranging gives:
n=ω2π
Substituting the value of ω:
n=125.712π≈125.716.28≈20revolutions/second
Step 7: Conclusion
The rate of rotation of the wheel is approximately 20 revolutions per second.
---
We are given:
- Length of the spokes (r) = 1 m
- Magnetic flux density (B) = 5×10−5T
- E.M.F (E) = 227mV=227×10−3V
The formula for the induced E.M.F in a rotating wheel is given by:
E=12Bωr2
where:
- E is the induced E.M.F,
- B is the magnetic flux density,
- ω is the angular velocity in radians per second,
- r is the radius (length of the spokes).
Rearranging the formula to solve for ω:
ω=2EBr2
Substituting the values into the equation:
ω=2×(227×10−3)5×10−5×(1)2
Calculating the numerator:
2×(227×10−3)=447×10−3
Calculating the denominator:
5×10−5×12=5×10−5
Now substituting these into the equation:
ω=447×10−35×10−5=44×10−37×5×10−5=44×10−335×10−5=4435×102=1.2571×102rad/s
Thus,
ω≈125.71rad/s
We know that:
ω=2πn
where n is the number of revolutions per second. Rearranging gives:
n=ω2π
Substituting the value of ω:
n=125.712π≈125.716.28≈20revolutions/second
The rate of rotation of the wheel is approximately 20 revolutions per second.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE EXERCISE (SELF INDUCTANCE AND MUTUAL INDUCTANCE)
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
39 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE EXERCISE (MAGNETIC FLUX, FARADAY.S LAW, LENZ.S LAW , AC GENERATOR)
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
When a wheel with metal spokes 1.2m long is rotated in a magnetic field of flux density 5×10−5T normal to the plane of the wheel, an e.m.f. of 10−2 volt is induced between the rim and the axle. Find the rate of rotation of the wheel.
View SolutionThe spokes of a wheel are made of metal and their lengths are of one metre. On rotating the wheel about its own axis in a uniform magnetic field of 5×10−5 tesla normal to the plane of the wheel, a potential difference of 3.14mV is generated between the rim and the axis. The rotational velocity of the wheel is-
View Solution
Knowledge Check
A wheel with 20 metallic spokes each of length 8.0 m long is rotated with a speed of 120 revolution per minute in a plane normal to the horizontal component of earth magnetic field H at a place. If H=0.4×10−4 T at the place, then induced emf between the axle the rim of the wheel is
A2.3×10−4VB3.1×10−4VC2.9×10−4VD1.61×10−4V
A rectangular coil having 60 turns and area of 0.4 m2 is held at right angles to a uniform magnetic field of flux density 5×10−5T. Calculate the magnetic flux passing through it.
View SolutionA wheel with ten metallic spokes each 0.50m long is rotated with a speed of 120rev/min in a plane normal to the earth's magnetic field at the place. If the magnitude of the field is 0.4 gauss, the induced e.m.f. between the axle and the rim of the wheel is equal to
View SolutionA wheel with ten metallic spokes each 0.50m long is rotated with a speed of 120rev/min in a plane normal to the earth's magnetic field at the place. If the magnitude of the field is 0.4 gauss, the induced e.m.f. between the axle and the rim of the wheel is equal to
View SolutionA wheel with ten metallic spokes each 0.50m long is rotated with a speed of 120rev/min in a plane normal to the earth's magnetic field at the place. If the magnitude of the field is 0.4 gauss, the induced e.m.f. between the axle and the rim of the wheel is equal to
View SolutionA proton enters a magnetic field of flux density 1.5 T with a velocity of 2×107ms−1 at an angle of 30° with the field. The force on the proton is [ep=1.6×10−19C]
View SolutionA wheel with 20 metallic spokes each 0.5 m long is rotated with a speed of 120 rev/min in a plane normal to the horizontal component of earth.s magnetic field HE at a place. If Hg =0.4 G at the place, what is the induced emf between the axle and the rim of the wheel ? Note that 1G= 10−4T.
View SolutionA wheel with 4 spokes is placed with its plane perpendicular to a uniform magnetic field B of magnitude 0.5 T. The field is directed into the plane of the paper and is present over the entire region of the wheel as shown in Fig. When the switch S is closed, there is initial current of 6 A between the axis and the rim and the wheel begins to rotate. Resistances of the spokes are 1, 2, 4 and 8 Ω, respectively. Resistance of rim is negligible.
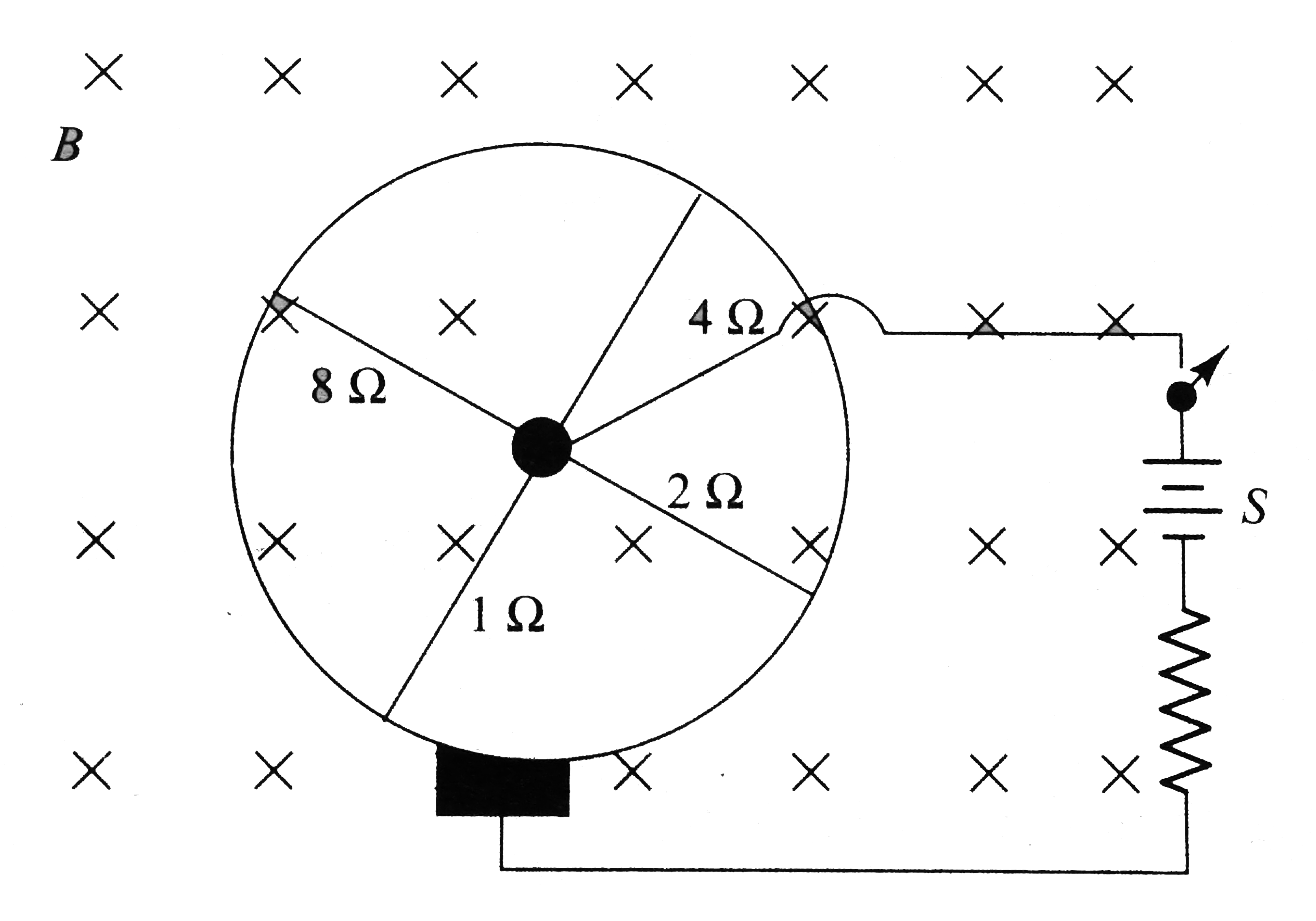
a. What is the direction of rotation of the wheel?
b. Radius of the wheel is 0.2 m. Calculate initial torque acting on the wheel.
View Solution
