A wave disturbance in a medium is described by . Where x and y are in m and t in sec. The values in Column-II are in SI units.
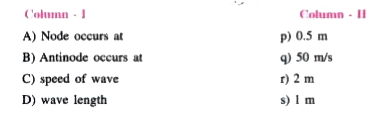
The correct Answer is:4
Step by step video solution for A wave disturbance in a medium is described by Y=0.02 cos( 50 pi t + pi/2) cos pi x . Where x and y are in m and t in sec. The values in Column-II are in SI units. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The coordinates of a particle moving in a plane are given by x (t) = a cos (pt) and y (t) = b sin (pt), where a, b (< a), and p are positive constants of appropriate dimensions. Then:
View SolutionThe equation of a wave disturbance is given as y=0.02cos(π2+50πt)cos(10πx), where x an y are in metre and t in second. Choose the wrong statement.
View SolutionThe wave described by y =0.25sin(10πx−2πt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionThe wave described by y=0.25sin(10πx−2πt) , where x and y are in metres and t in seconds , is a wave travelling along the:
View SolutionThe equation of a wave distrubance is a given as y=0.02sin(π2+50πt)cos(10πx), where x and y are in metre and t is in second . Choose the correct statement (s).
View SolutionA stationary wave is given by y=5sin(πx)3cos40πt where x and y are in cm and t is in seconds
What is the distance between two successive nodes
View SolutionThe equation of stationary wave along a stretched string is given by y=5sin(π3x)cos40πt where x and y are in centimetre and t in second. The separation between two adjacent nodes is :
View SolutionA stationary wave is given by y=5sin(πx)3cos40πt where x and y are in cm and t is in seconds
What is the velocity of a particle of the string at the position x = 1.5 cm when t=98s
View SolutionA wave is represented by the equation y=Asin(10πx+15πt+π6) wher x is in metre and t in second. The expression represents
View SolutionA wave is represented by the equation :y=Asin(10πx+15πt+π/3) where, x is in metre and t is in second. The expression represents.
View Solution
