A pith ball of mass 9×10−5 kg carries a charge of 5μC. What must be charge in another pith ball placed directly 2 cm above the given pith ball such that they held in equilibrium?
3.2×10−11C
7.84×10−12C
1.2×10−13C
1.6×10−19C
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Calculate the weight of the first pith ball
The weight W of the first pith ball can be calculated using the formula:
W=m⋅g
where:
- m=9×10−5kg (mass of the pith ball)
- g=9.8m/s2 (acceleration due to gravity)
Substituting the values:
W=9×10−5kg×9.8m/s2=8.82×10−4N
Step 2: Set up the equation for electrostatic force
The electrostatic force F between two charges can be calculated using Coulomb's law:
F=14πϵ0q1⋅q2d2
where:
- ϵ0=8.85×10−12C2/N m2 (permittivity of free space)
- q1=5μC=5×10−6C (charge of the first pith ball)
- d=2cm=0.02m (distance between the two pith balls)
Substituting the values into the formula:
F=9×109⋅(5×10−6)⋅q2(0.02)2
Step 3: Equate weight and electrostatic force
For the pith balls to be in equilibrium, the weight of the first pith ball must equal the electrostatic force:
W=F
Substituting the expressions we have:
8.82×10−4=9×109⋅(5×10−6)⋅q2(0.02)2
Step 4: Solve for q2
Rearranging the equation to solve for q2:
q2=8.82×10−4⋅(0.02)29×109⋅(5×10−6)
Calculating (0.02)2:
(0.02)2=0.0004
Now substituting this back into the equation:
q2=8.82×10−4⋅0.00049×109⋅5×10−6
Calculating the numerator:
8.82×10−4⋅0.0004=3.528×10−7
Calculating the denominator:
9×109⋅5×10−6=4.5×104
Now substituting these values:
q2=3.528×10−74.5×104=7.84×10−12C
Final Answer
Thus, the charge on the second pith ball must be:
q2=7.84×10−12C
The weight W of the first pith ball can be calculated using the formula:
W=m⋅g
where:
- m=9×10−5kg (mass of the pith ball)
- g=9.8m/s2 (acceleration due to gravity)
W=9×10−5kg×9.8m/s2=8.82×10−4N
The electrostatic force F between two charges can be calculated using Coulomb's law:
F=14πϵ0q1⋅q2d2
where:
- ϵ0=8.85×10−12C2/N m2 (permittivity of free space)
- q1=5μC=5×10−6C (charge of the first pith ball)
- d=2cm=0.02m (distance between the two pith balls)
F=9×109⋅(5×10−6)⋅q2(0.02)2
For the pith balls to be in equilibrium, the weight of the first pith ball must equal the electrostatic force:
W=F
Substituting the expressions we have:
8.82×10−4=9×109⋅(5×10−6)⋅q2(0.02)2
Rearranging the equation to solve for q2:
q2=8.82×10−4⋅(0.02)29×109⋅(5×10−6)
(0.02)2=0.0004
q2=8.82×10−4⋅0.00049×109⋅5×10−6
8.82×10−4⋅0.0004=3.528×10−7
9×109⋅5×10−6=4.5×104
q2=3.528×10−74.5×104=7.84×10−12C
Thus, the charge on the second pith ball must be:
q2=7.84×10−12C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I
80 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
A small ball of mass 2×10−3kg, having a charge 1μC, is suspended by a string of length 0.8m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution.
View SolutionTwo positively charged particles each of mass is 9×10−30kg and carrying a charge of 1.6×10−19C are placed at a distance .r. apart. If each experiences a force equal to its weight, the value of r is (g=10ms−2)
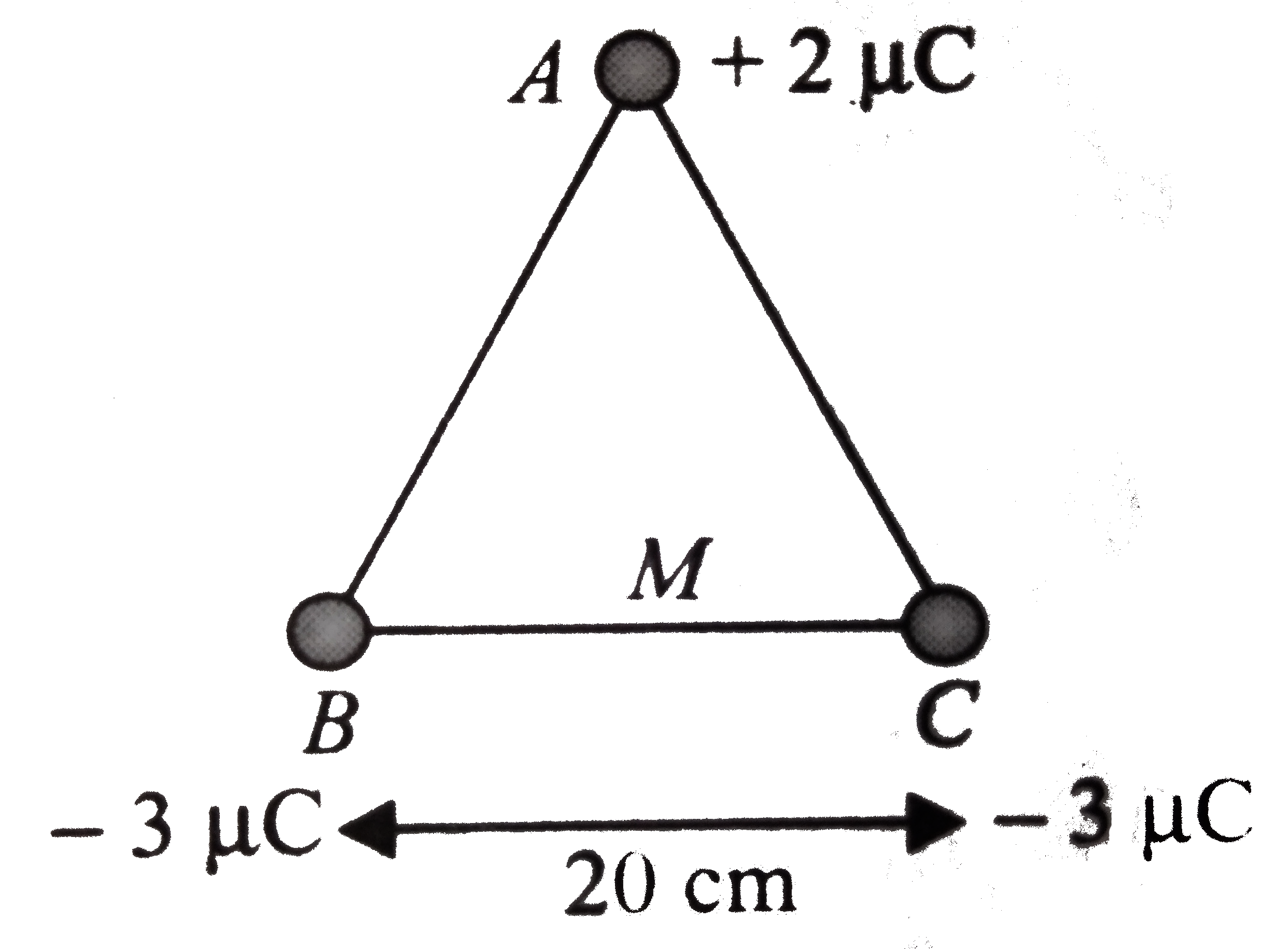
View SolutionThree point charges of +2μC,−3μC , and −3μC are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionTwo identical small equally charged conducting balls are suspended from long threads secured at one point. The charges and masses of the balls are such that they are in equilibrium when the distance between them is a(the length of thread L>>a). Then one of the balls is discharged. what will be the distance b(b<<L) between the balls when equilibrium is restored?
View SolutionA ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mas 1.0 kg. After the collision the balls stick together ane remain motionless. What was the velocity of the 1.0 kg block before the collision?
View SolutionIf three uniform spheres, each having mass M and radius R, are kept in such a way that each touches the other two, the magnitude of the gravitational force on any sphere due to the other two is:
View SolutionA 0.50 gm ball carries a charge of magnitude 10μC. It is suspended by a string in a downward electric field of intensity 300N/C. If the charge on the ball is positive, then the tension in the string is (g=10ms−2)
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View Solution
