A parallel - plate capacitor, filled with a dielectric of dielectric constant k, is charged to a potential V0. It is now disconnected from the cell and the slab is removed. If it now discharges, with time constant τ, through a resistance, then find time after which the potential difference across it will be V0?
To solve the problem step by step, we will analyze the situation of the parallel-plate capacitor filled with a dielectric and how it discharges after the dielectric is removed.
Step 1: Understand the Initial Conditions
The capacitor is initially charged to a potential V0 with a dielectric of dielectric constant k. The capacitance with the dielectric is given by:
C′=kC
where C is the capacitance without the dielectric.
Step 2: Calculate the Initial Charge
The charge Q0 on the capacitor when it is charged to V0 is:
Q0=C′V0=kCV0
Step 3: Remove the Dielectric
After disconnecting from the cell and removing the dielectric, the capacitance returns to:
C=C′
The charge Q on the capacitor at any time t during discharge can be described by the formula:
Q=Q0e−t/τ
where τ is the time constant of the circuit.
Step 4: Relate Charge to Voltage
The potential difference across the capacitor at time t is given by:
V(t)=QC
Substituting for Q:
V(t)=Q0e−t/τC
Step 5: Set Up the Equation for Voltage
At time t, we want the potential difference V(t) to equal V0:
V(t)=V0
Substituting the expression for V(t):
Q0e−t/τC=V0
Substituting Q0=kCV0:
kCV0e−t/τC=V0
This simplifies to:
kV0e−t/τ=V0
Step 6: Simplify the Equation
Dividing both sides by V0 (assuming V0≠0):
ke−t/τ=1
Step 7: Solve for Time t
Taking the natural logarithm on both sides:
e−t/τ=1k
Taking the logarithm:
−tτ=ln(1k)
This simplifies to:
−tτ=−ln(k)
Thus, we find:
t=τln(k)
Final Answer
The time after which the potential difference across the capacitor will be V0 is:
t=τln(k)
The capacitor is initially charged to a potential V0 with a dielectric of dielectric constant k. The capacitance with the dielectric is given by:
C′=kC
where C is the capacitance without the dielectric.
The charge Q0 on the capacitor when it is charged to V0 is:
Q0=C′V0=kCV0
After disconnecting from the cell and removing the dielectric, the capacitance returns to:
C=C′
The charge Q on the capacitor at any time t during discharge can be described by the formula:
Q=Q0e−t/τ
where τ is the time constant of the circuit.
The potential difference across the capacitor at time t is given by:
V(t)=QC
Substituting for Q:
V(t)=Q0e−t/τC
At time t, we want the potential difference V(t) to equal V0:
V(t)=V0
Substituting the expression for V(t):
Q0e−t/τC=V0
Substituting Q0=kCV0:
kCV0e−t/τC=V0
This simplifies to:
kV0e−t/τ=V0
Dividing both sides by V0 (assuming V0≠0):
ke−t/τ=1
Taking the natural logarithm on both sides:
e−t/τ=1k
Taking the logarithm:
−tτ=ln(1k)
This simplifies to:
−tτ=−ln(k)
Thus, we find:
t=τln(k)
The time after which the potential difference across the capacitor will be V0 is:
t=τln(k)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
58 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
A capacitor of capacitance 10μF is charged to a potential 50V with a battery. The battery is now disconnected and an additional charge 200μC is given to the positive plate of the capacitor. The potential difference across the capacitor will be.
View SolutionA parallel-plate capacitor is filled with a delectric meterial having resistivity(ρ)and dielectric constant K.The capcitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric.Show that the time constant of the discharge is independent of all gepmetrical parameters like the plate area or separation between the plates. Find this time constant.
View Solution
Knowledge Check
A parallel plate condenser with a dielectric of dielectric constant K between the plates has a capacity C and is charged to a potential V volt. The dielectric slab is slowly removed from between the plates and then reinserted. The net work done by the system in this process is
AzeroB12(K−1)CV2CCV2(K−1)KD(K−1)CV2
A parallel plate capacitor has a dielectric (of dielectric constant k) between the plates. The plates are charged to a surface charge density σ0. What is the density of the polarized charge that appear on the surface of the dielectric.
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionAn uncharged parallel plate capacitor having a dielectric of dielectric constant K is connected to a similar air core parallel plate capacitor charged to a potential V0. The two share the charge, and the common potential becomes V. The dielectric constant K is
View SolutionA capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

View SolutionA parallel plate capacitor charged to potential difference V0 . The variation of potential V from x= 0 to x= d is best described by
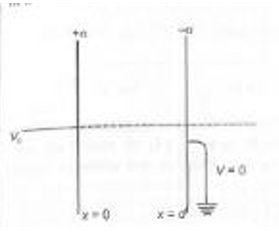
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitor with air as dielectric is charged to a potential .v. using a battery . Removing the battery. The charged capacitor is then connected across an identical uncharged parallel plate capacitor filled with was of dielectric constant k. The common potential of both the capacitor is
View Solution
