A body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
t1/2
t
t3/2
t2
The correct Answer is:B
Step by step video solution for A body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Projectile motion is a two dimensional motion with constant acceleration. Is this statement true or false?
View SolutionA body initially at rest travels a distance 100 m in 5 s with a constant acceleration. Calculate : (i) the acceleration, and (ii) the final velocity at the end of 5 S.
View Solution
Knowledge Check
For the one dimensional motion, described by x=t−sint
Ax(t)>0 for all t gt 0Bν(t)>0 for all t>0Ca(t)>0 for all t>0Dall of these
A body starts from rest and acquires velocity V in time T. The instantaneous power delivered to the body in time 't' proportional to
View SolutionA body, initially at rest, starts moving with a constant acceleration 2 ms−2. Calculate : (i) the velocity acquired and (ii) the distance travelled in 5 s.
View SolutionA particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
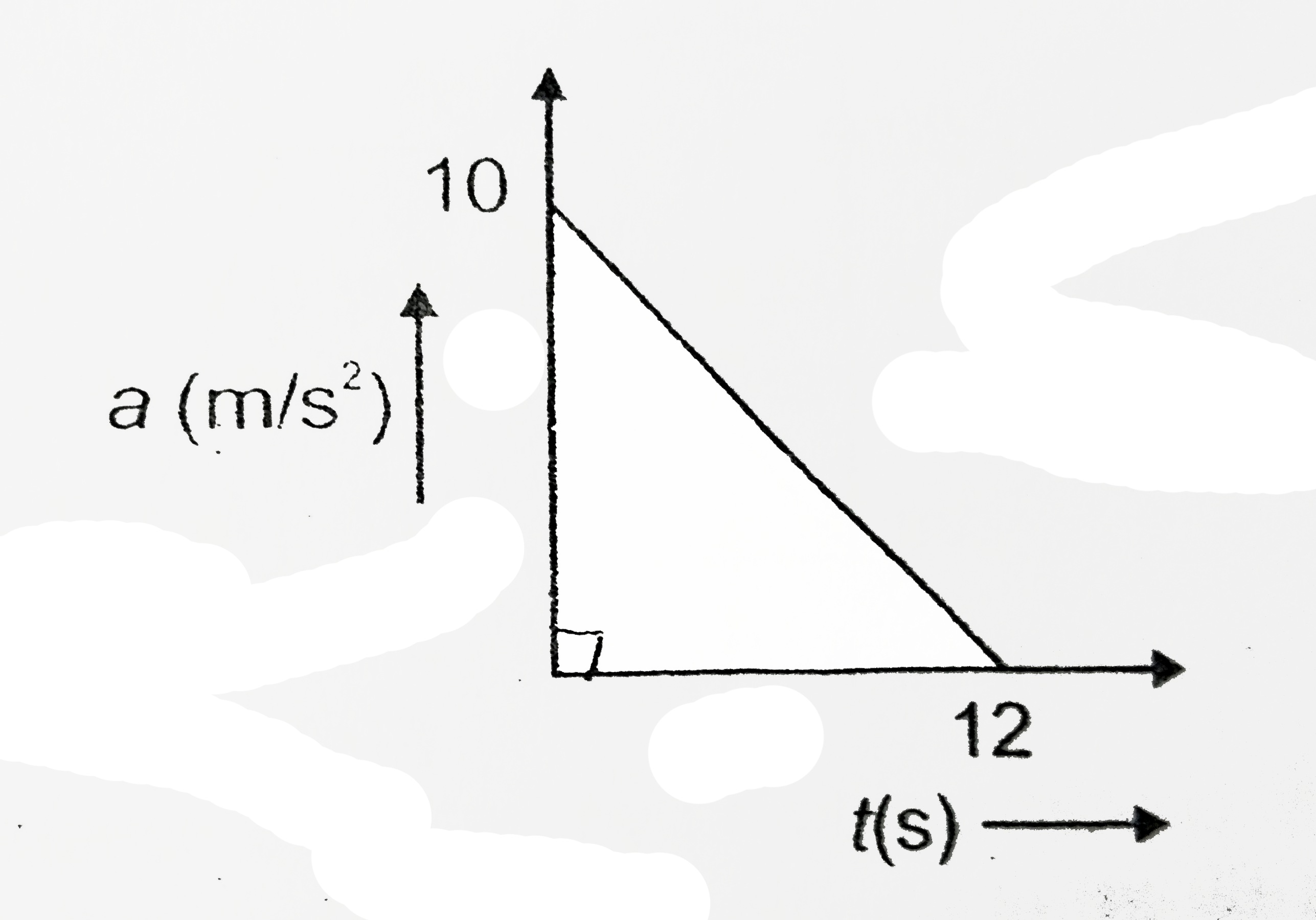
View SolutionAssertion : Simple harmonic motion is an example on one dimensional motion with non-uniform acceleration .
Reason : In simple harmonic motion, acceleration varies with displacement linearly.
View SolutionAn insect of mass m moves up along a hanging stationary thread, with acceleration a. Find the power delivered by the gravity after a time t.
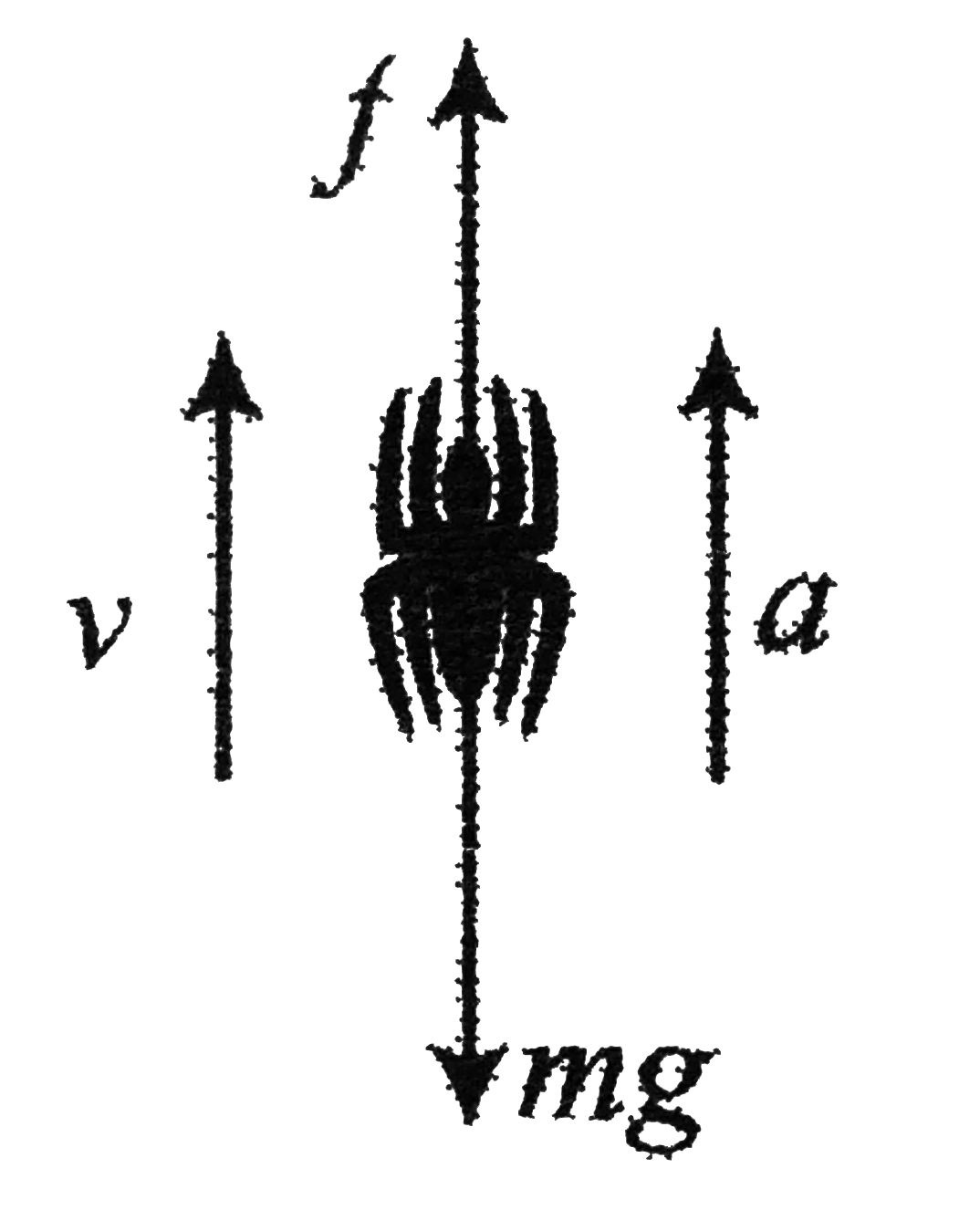
View SolutionA motor drives a body along a straight line with a constant force. The power P developed by the motor must vary with time t as
View SolutionA variable force F acts on a body which is free to move. The displacement of the body is proportional to t3, where t = time. The power delivered by F to the body will be proportional to
View Solution
