A ball of a mass m hits the floor with as speed v making an angle of incidence θ with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
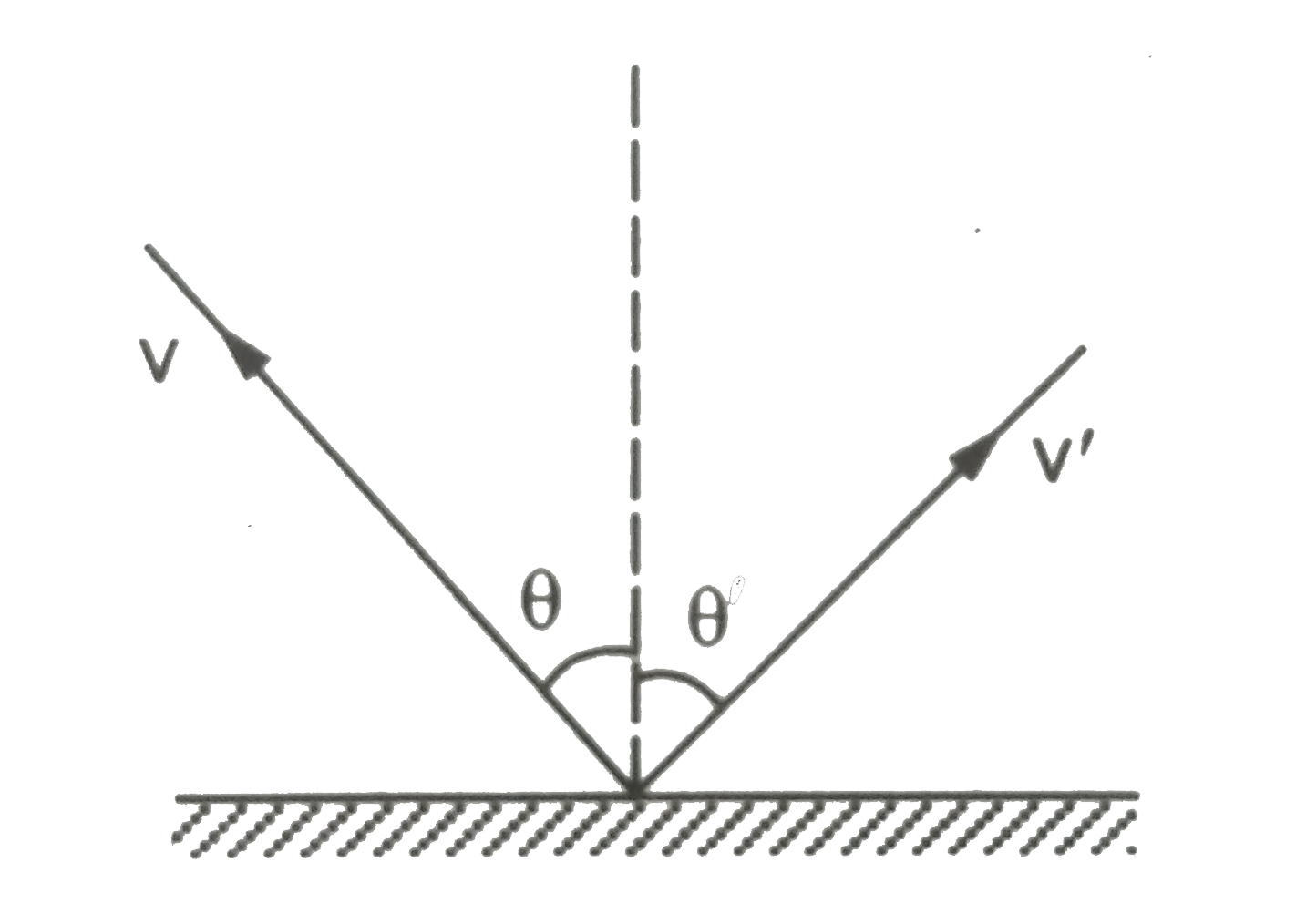
Suppose the angle of reflection is θ. and the speed after the collision is v.. The floor exerts a force on the ball along the normal during the collision. There is no force parallel to the surface. Thus, the parallel component of the velocity of the ball remains unchanged.
This gives v. in θ. = v sin θ ......(i)
For the components normal to the floor, the velocity of separation is v. cos θ. and the velocity of approach is v cos θ.

Hence, v. cos θ. = ev cos θ .....(ii)
From (i) and (ii),
v.=v√sin2θ+e2cos2θ
and tanθ.=tanθe⇒e=tanθtanθ1
Similar Questions
A ball of mass m hits a floor with a speed v0 making an angle of incidence α with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
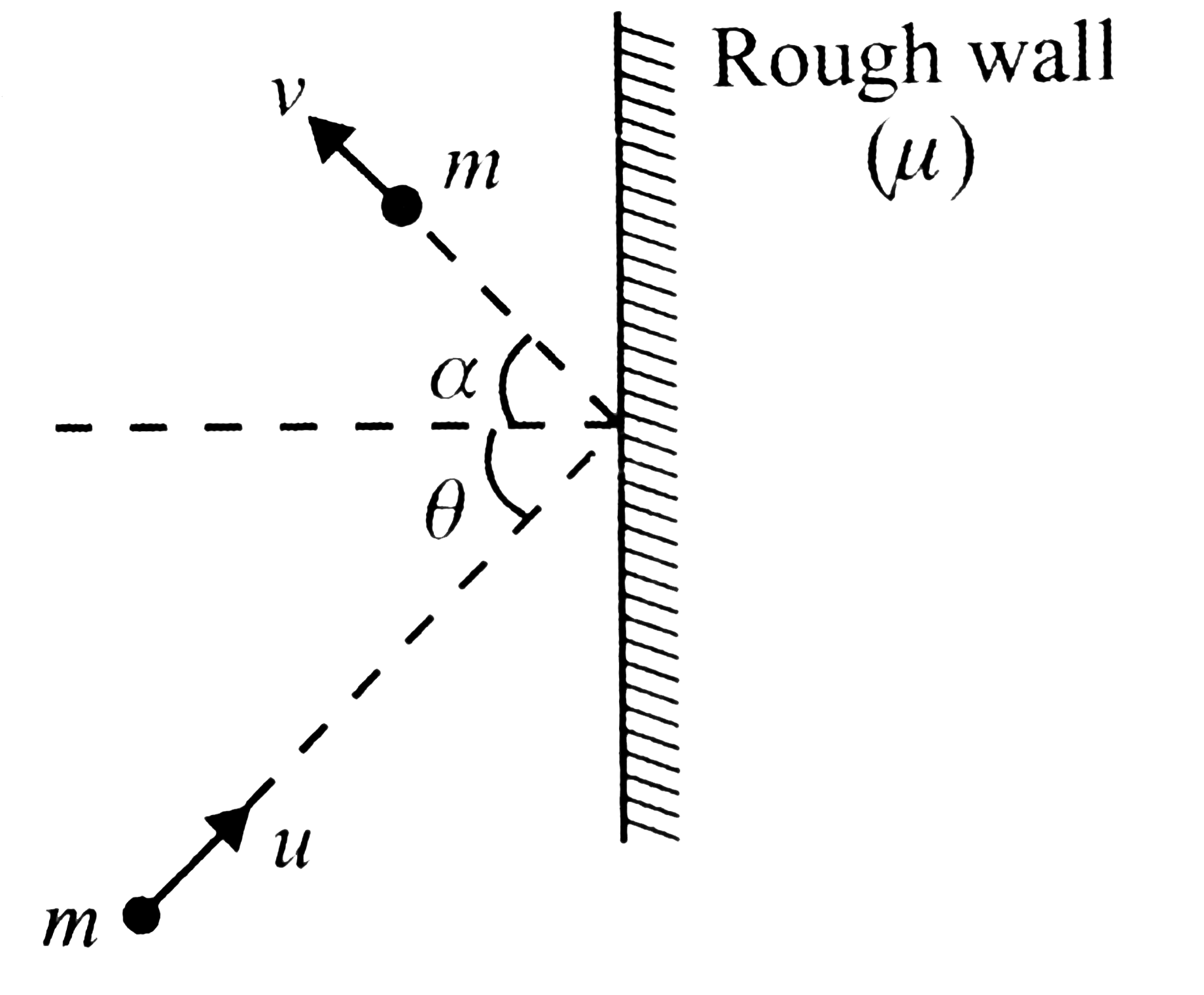
A small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
View SolutionA ball strickes a horizontal floor at an angle θ=45∘ with the normal to floor. The coefficient of restitution between the ball and the floor is e=1/2. The fraction of its kinetic energy lost in the collision is.
View SolutionA ball strickes a horizontal floor at an angle θ=45∘ with the normal to floor. The coefficient of restitution between the ball and the floor is e=1/2. The fraction of its kinetic energy lost in the collision is.
View SolutionTwo balls of equal mass have a head-on collision with speed 6m/s. If the coefficient of restitution is 13, find the speed of each ball after impact in m/s
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution
