A nail is located below the point of suspensions of a simple pendlum of length .l.. The bob is released from horizontal position. If the bob loops a verticle circle with nail as centre, find the distance of nail from point of suspension.
Form the principle of conservation of mechanical energy
PE at the horizontal position = KE at the lowest position.
mgl=12mv2
To loop the vertical circle ,
v2=5g(1−x) where .x. is the distance of nail from point of suspension, and .v. is the velocity at lowest point of path.
(mgl=12m.5g(l−x)),l=52(l−x), x=3l/5
Similar Questions
A simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionThe bob of a simple pendulum of length l dropped from a horizontal position strikes a block of the same mass elastically, placed on a horizontal table (frictionless) as shown in the diagram, the block shall have kinetic energy-

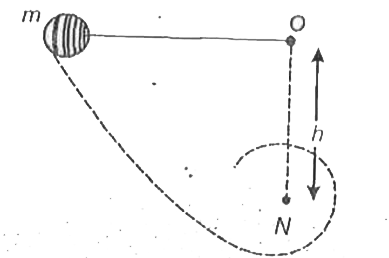
View SolutionA particle of mass m attached to the end of string of length l is released from the horizontal position. The particle rotates in a circle about O as shown When it is vertically below O, the string makes contact with a nail N placed directly below O at a distance h and rotates around it. For the particle to swing completely around the nail in a circle.
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View SolutionA pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
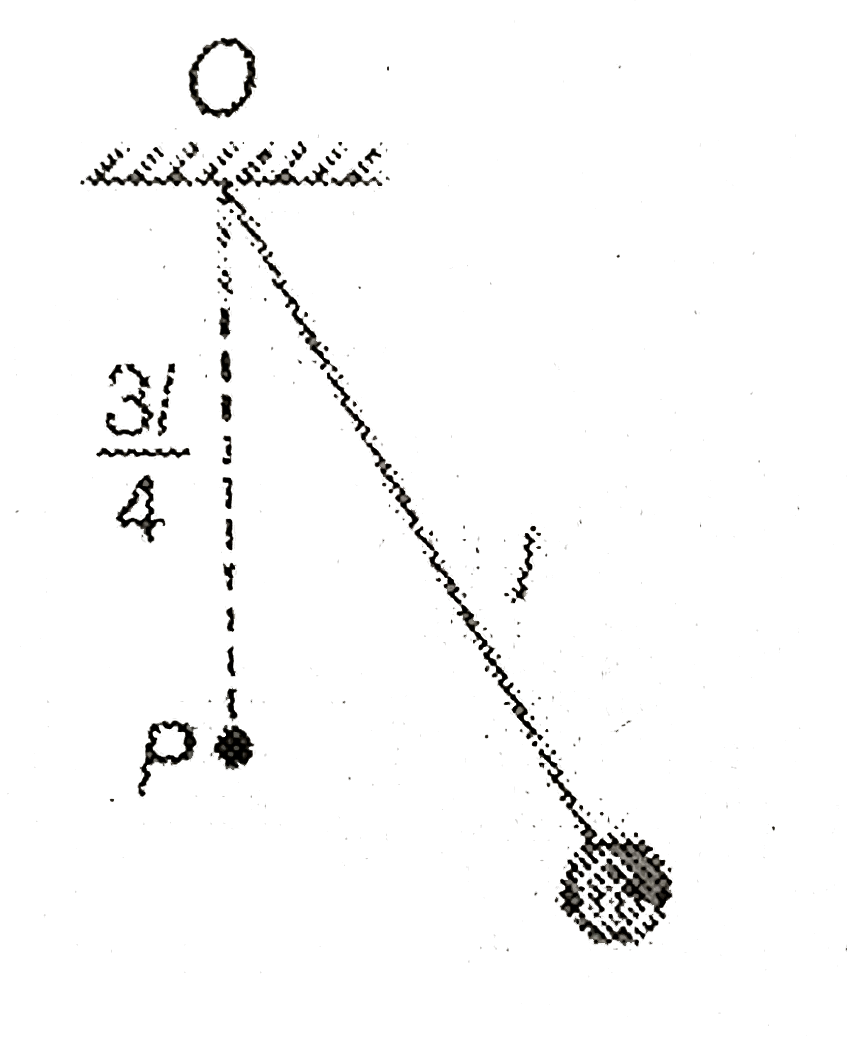
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View SolutionIn the given system, when the ball of mass m is released, it will swing down the dotted arc.
a. How fast will it reach the lowest point in its swing? A nail is located at a distance d below the point of suspension.
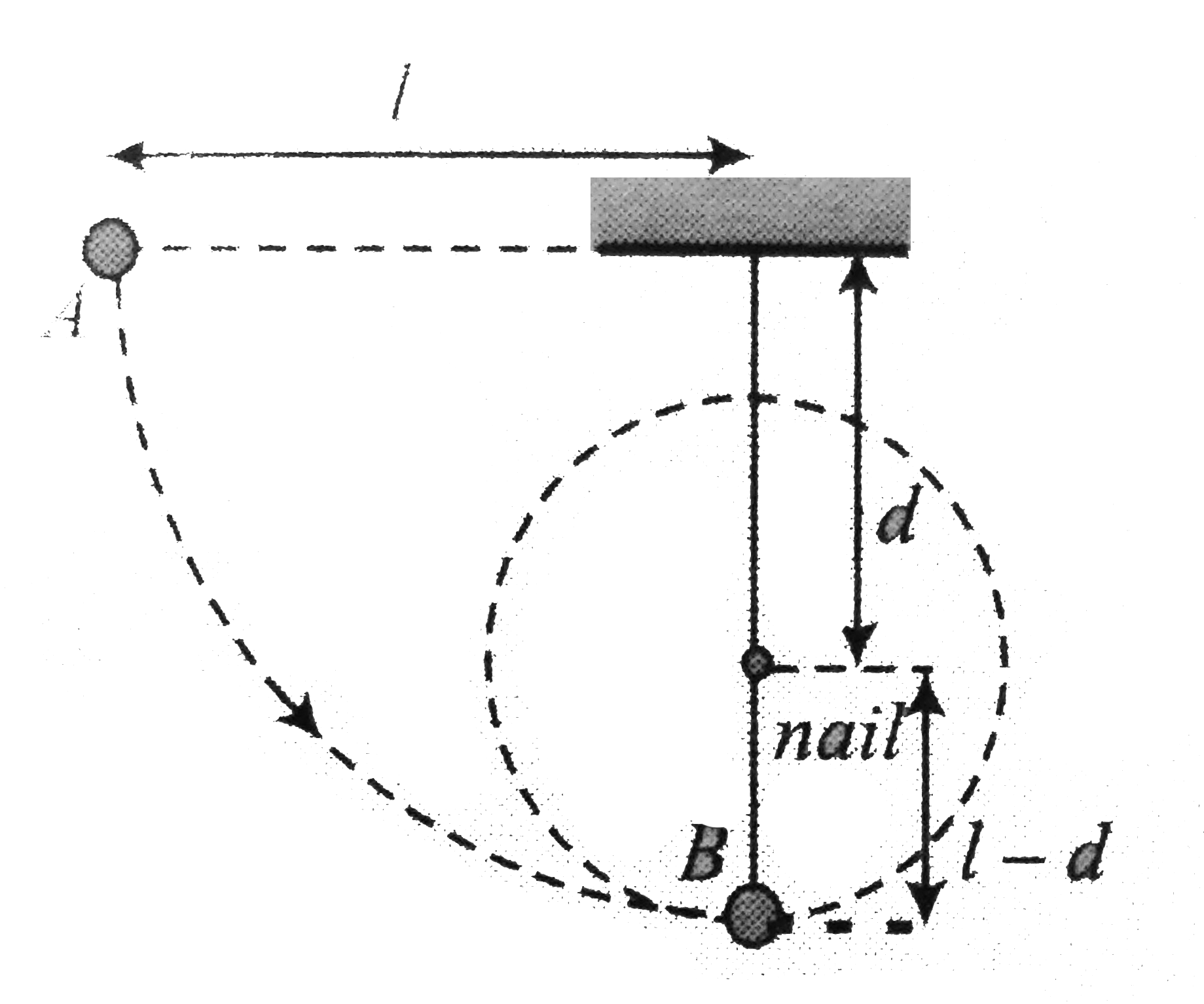
b. Show that d must at 0.6l, if the ball is to swing completely around a circle centered along the nail.
c. If d=0.6l, find the change in tension in the string just after it touches the nail.
View SolutionA simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight w of the bob about the point of suspension. When is the torque zero?
View Solution
