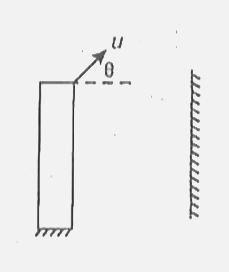
A boy throws a ball with initial velocity $u$ at an angle of projection $θ$ from a tower of height H.
Neglecting air resistance, find
a. How high above the building the ball rises
b. Its speed just before it hits the ground.

Video Solution

Text Solution

Verified by Experts

(a) Only gravitational force acts on the ball, which is conservative , therefore we can apply conservation of energy. We assign reference level at the top of the building i.e., $U_{g i} = 0$ . At the topmost point in the path, the ball is moving horizontally with velocity $u cos θ$ . Initial total mechanical energy :
$E_{i} = 0 + \frac{1}{2} m u^{2}$
Total mechanical energy at the topmost point :
$E_{f} = \frac{1}{2} m u^{2} {cos}^{2} θ + m g h$
From conservation of energy, we have $E_{i} = E_{f}$
(a) $\frac{1}{2} m u^{2} = \frac{1}{2} m u^{2} {cos}^{2} θ + m g h$
or $h = \frac{u^{2} - u^{2} {cos}^{2} θ}{2 g}$
(b) If v is the speed of the ball at the ground,
$E_{f} = \frac{1}{2} m v^{2} - m g h$
From conservation of energy, we have
$E_{i} = E_{f} \Rightarrow \frac{1}{2} m u^{2} = \frac{1}{2} m v^{2} m g H, v = \sqrt{u^{2} + 2 g H}$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile