A light rod of length 2m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross sectional area 0.1 sq. cm and the other is of brass of cross-sectional area 0.2 sq. cm find out the position along te rod at which a weight may be hung to produce equal stresses in both wires. Y for steel =20×1011 dyne cm−2 and Y for brass =10×1011 dyne m−2
Suppose a1 and a2 are the cross-sectional areas, and Y1 and Y2 are the Young.s moduli of steel and brass wire respectively. Let T1 and T2 are tensions in the steel and brass wires respectively.
Let x is distance of the position of the hanging weight from the steel wire.
i) First case : For equal stress in both wires, we have
T1a1=T2a2
T110−3=T22×10−3 or T2=2T1 ....(i)
As the whole system is in equilibrium, so ∑→τ=0. Taking moment of all the forces acting on the rod about C, we have
T1x=T2(2−x)=0 ....(ii)
Solving eqn (i) and (ii)
we get x=43m
ii) second case :
For equal strain in both the wires e1=e2
T1la1Y1=T2la2Y2
T110−3×2×1011=T22×10−3×1011
T1=T2 ...(iii)
From equation (ii) and (iii) , we get x = 1m
Similar Questions
A light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]

View SolutionA light rod of length 2m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section 0.1cm2. The other wire is a brass of cross section 0.2cm2. A weight is suspended from a certain point of the rod such that equal stress are produced in both the wires. Which of the following are correct?
View Solution
Knowledge Check
A light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wireIn the question number 36, at which distance a weight may be hung along the rod, in order to produce equal strains in both the wires?
A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
A light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA 2 m long light metal rod AB is suspened form the c eiling horizontally by means of two vertices wires of equal length, tied to the ends. One brass and has corss section of 0.3×10−4m2 and the other is of steel with 0.1×10−4m2 corss-section. In order to have equal stresses in the two wires, a weight is hung from the rod. The position of weight along the rod from end A should be.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
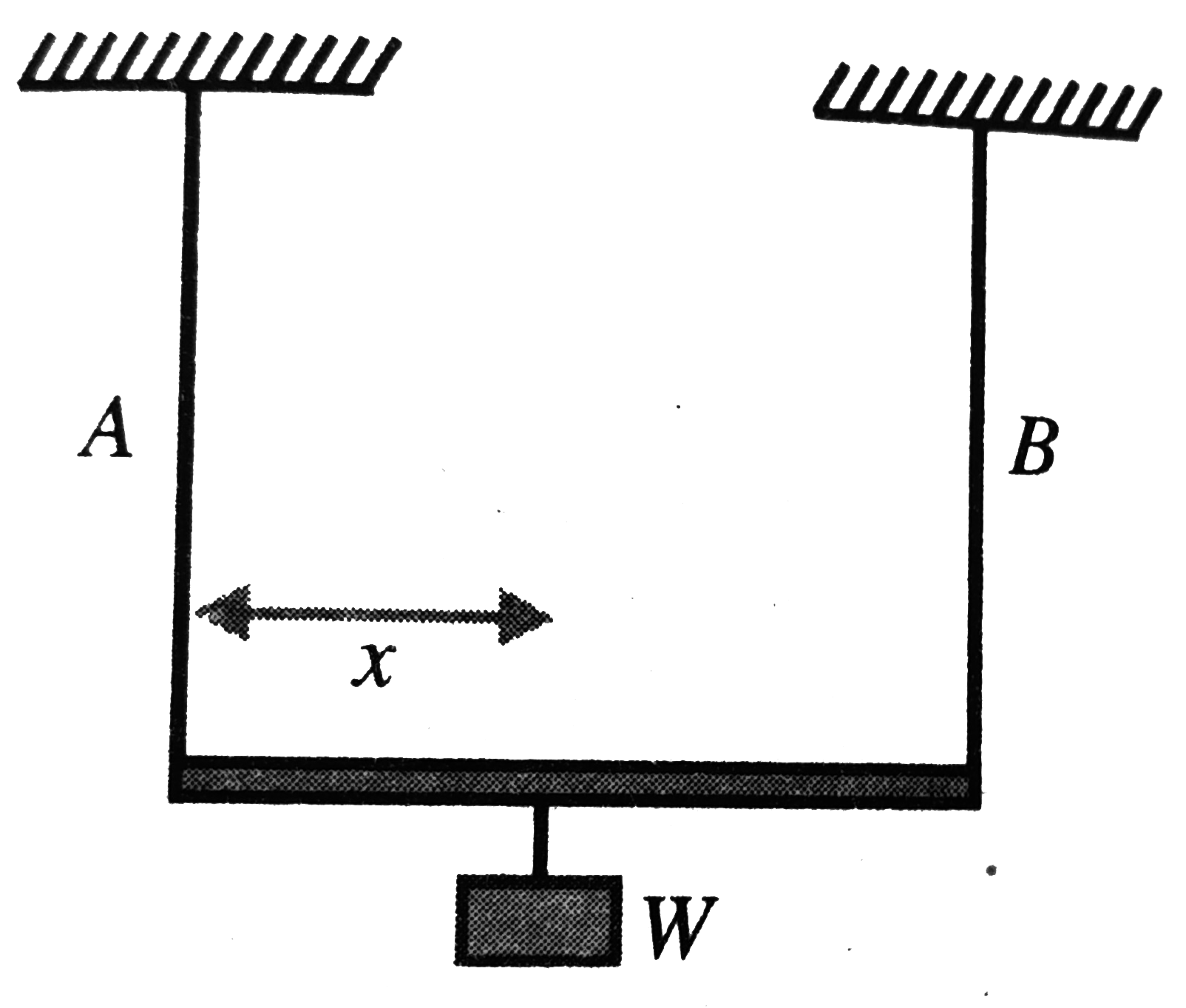
Determine the value of x so that equal stresses are produced in each wire.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
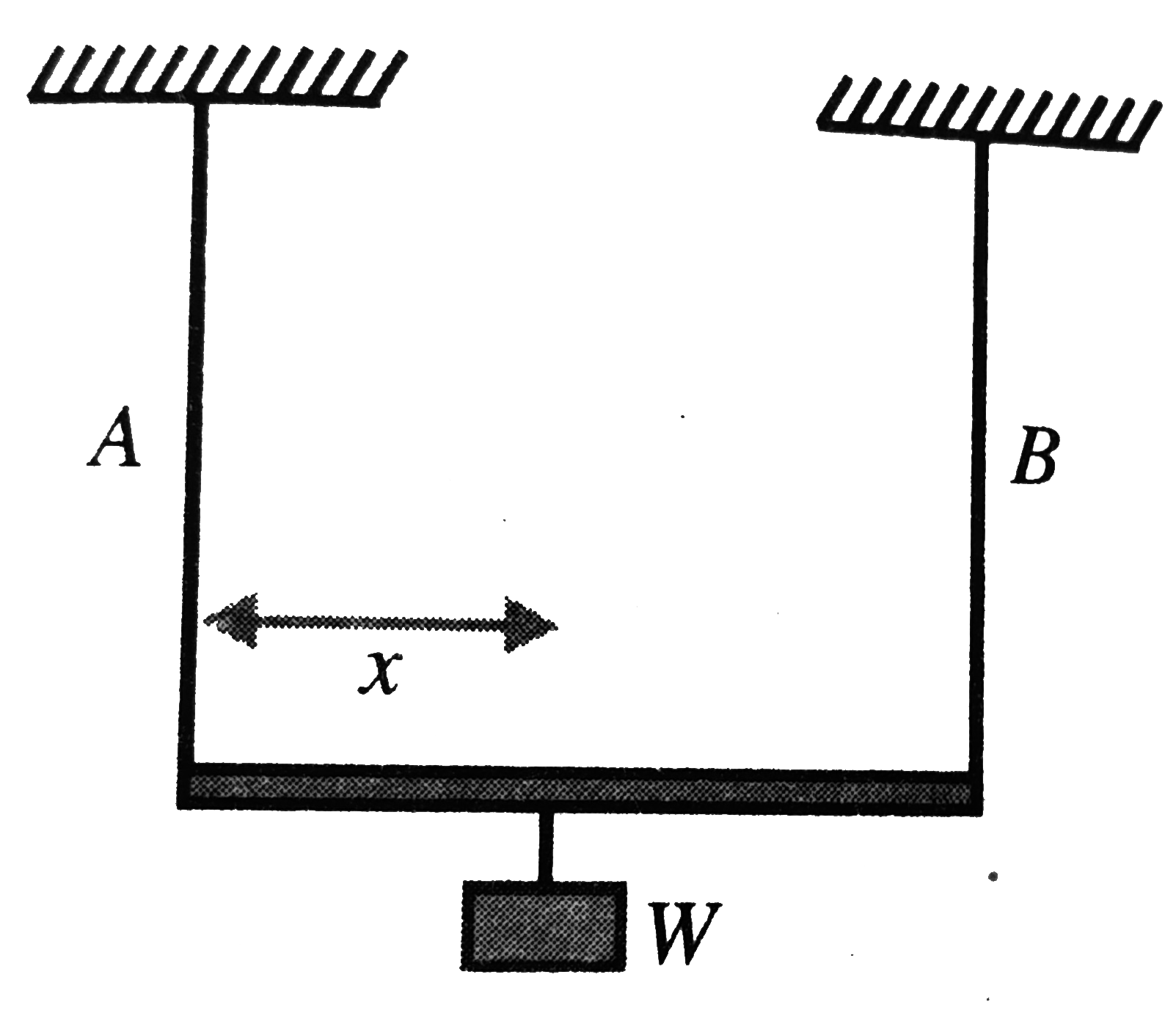
Determine the value of x so that equal strains are produced in each wire
View SolutionA wire of cross-sectional area A breaks due to its own weight when length of the wire is l. If area of cross-section of the wire is made 3A then maximum length of the wire can be hung without breaking is
View Solution
