At t=0, a force F = kt is applied on a block of mass m making an angle α with the horizontal . Suppose surfaces to be smooth. Find the velocity of the body at the time of breaking off the plane.

The free body diagram of mass m is shown in figure . For vertical equilibrium
Fsinβ+N=mg(or)AsF=kt
∴ktsinβ+N=mg........... (1)
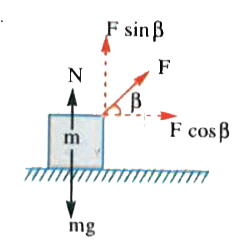
Equation of motion of mass m is Fcosβ=ma
orktcosβ=mdvdt(as a=dvdt),dv=ktmcosβdt
Integrating ∫v0dv=kmcosβ∫t0dt
[v]v0=kmcosβ[t22]t0⇒v=kcosβ2mt2 ........... (2)
At the moment of breaking off the plane N =0 . If τ is the corresponding time , then
∴ From (1) kτsinβ=mgorτ=mgksinβ........... (3)
∴ The velocity at the moment of breaking off the plane is given by putting t=τ in equation ( 2) , so (v=v0)
v0=kcosβ2mτ2=kcosβ2m(mgksinβ)2
∴v0=mg2cosβ2ksin2β
(b) Equation (2) may be expressed as dxdt=kcosβ2mt2
Integrating [x]x0=kcosβ2m[t33]t0
∴x=kcosβ6mt3
When the body breaks off the plane , we have
∴x0=kcosβ6m(mgksinβ)3=m2g3cosβ6k2sin3β
Similar Questions
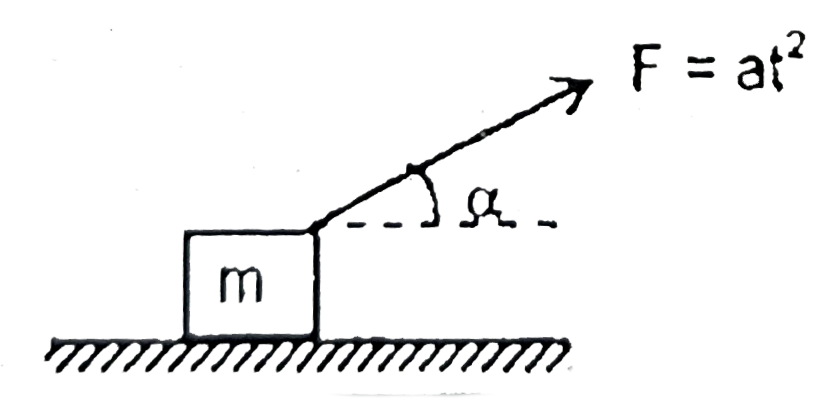
At t=0, a force F=at2 is applied to a small body of mass m at an angle α resting on a smooth horizontal plane
View SolutionIn the Fig force F=αt is applied on the block of mass m2. Here α is a constant and t is the time .Find the acceleration of the block Also draw the acceleration time graph of both the block

View SolutionA force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block

View SolutionA horizontal force F is applied to a block of mass m on a smooth fixed inclined plane of inclination θ to the horizontal as shown in the figure. Resultant force on the block up the plane is:

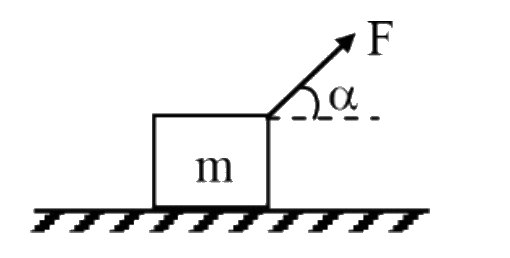
View SolutionAt the moment t = 0 , the force F = kt is applied to a small body of mass 'm' resting on a smoth horizontal plane. (K is a positive constant ). The direction of the force an angle θ with the horizontal always as shown

The distance travelled x by the body along horizontal before it leaves contact with the horizontal at t=t0 can be expressed in relation with time 't' as
View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle θ=37∘, with horizontal as shown in fig. find the acceleration of the block at the given instant.

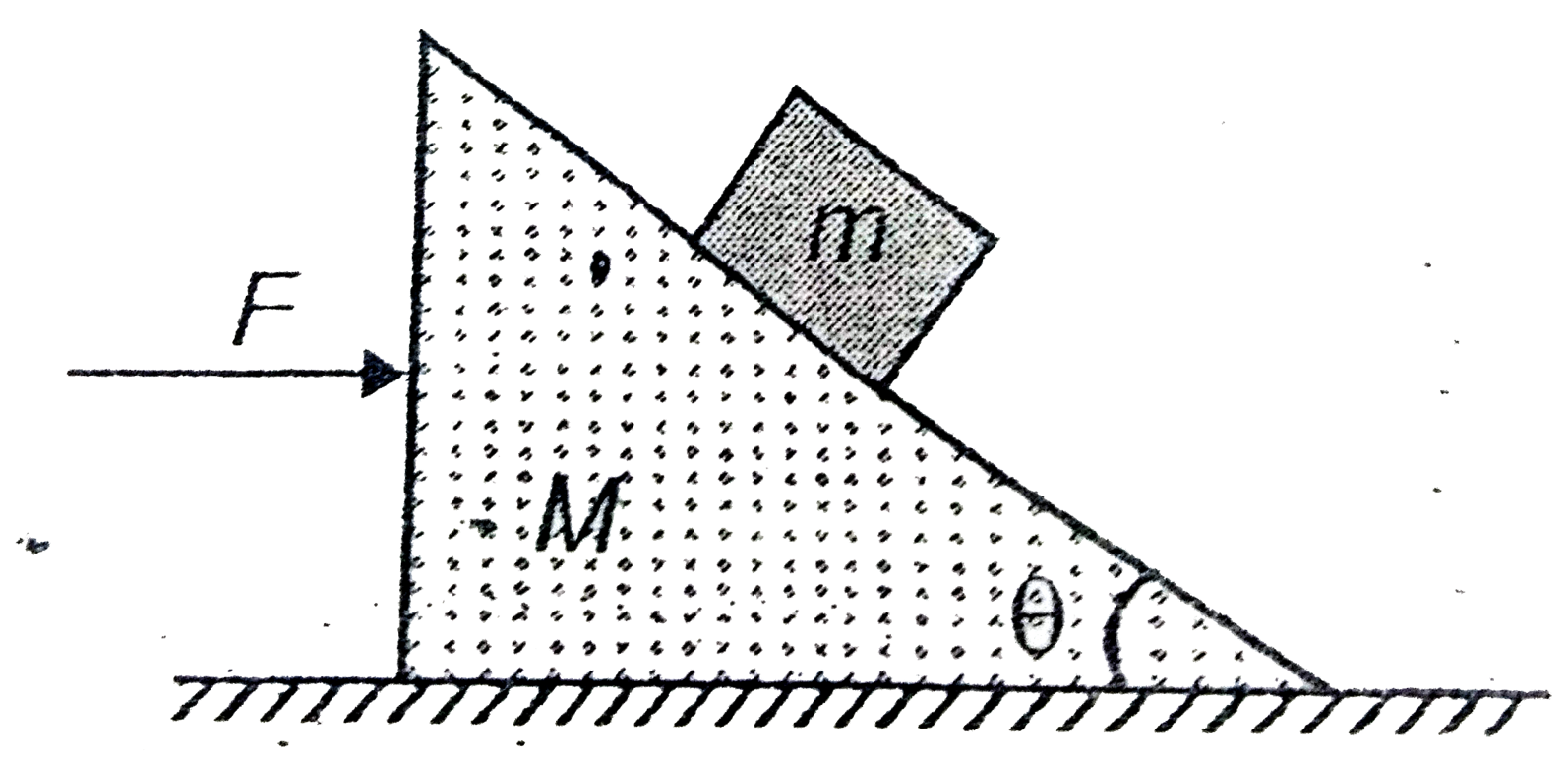
View SolutionA block of mass m is placed on a wedge of mass M and a force F is acting on its as shown . If all surfaces are smooth , find the force F such that, there is no relative motion between m and M.
View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.

View Solution
