A body moving in a curved path possesses a velocity 3 m/s towards north at any instant of its motion .After 10s ,the velocity of the body was found to be 4 m/s towards west.Calculate the average acceleration during this interval.
To solve the problem, we need to calculate the average acceleration of a body moving in a curved path, given its initial and final velocities.
1. Identify Initial and Final Velocities:
- The initial velocity v1 is given as 3 m/s towards the north. We can represent this as:
v1=3^im/s
- The final velocity v2 is given as 4 m/s towards the west. We can represent this as:
v2=4^jm/s
2. Calculate the Change in Velocity:
- The change in velocity Δv can be calculated using the formula:
Δv=v2−v1
- Substituting the values:
Δv=(4^j−3^i)m/s=−3^i+4^jm/s
3. Calculate the Magnitude of Change in Velocity:
- The magnitude of Δv is given by:
|Δv|=√(−3)2+(4)2=√9+16=√25=5m/s
4. Determine the Time Interval:
- The time interval Δt is given as 10 seconds.
5. Calculate the Average Acceleration:
- The average acceleration aavg can be calculated using the formula:
aavg=ΔvΔt
- Substituting the values:
aavg=5m/s10s=0.5m/s2
Final Answer:
The average acceleration during this interval is:
aavg=0.5m/s2
- The initial velocity v1 is given as 3 m/s towards the north. We can represent this as:
v1=3^im/s
- The final velocity v2 is given as 4 m/s towards the west. We can represent this as:
v2=4^jm/s
- The change in velocity Δv can be calculated using the formula:
Δv=v2−v1
- Substituting the values:
Δv=(4^j−3^i)m/s=−3^i+4^jm/s
- The magnitude of Δv is given by:
|Δv|=√(−3)2+(4)2=√9+16=√25=5m/s
- The time interval Δt is given as 10 seconds.
- The average acceleration aavg can be calculated using the formula:
aavg=ΔvΔt
- Substituting the values:
aavg=5m/s10s=0.5m/s2
The average acceleration during this interval is:
aavg=0.5m/s2
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)
22 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)
29 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
View SolutionA particle is moing with a velocity of 10m/s towards east. After 10s its velocity changes to 10m/s towards north. Its average acceleration is:-
View SolutionA body is moving with velocity 30m/s towards east. After 10s its velocity becomes 40m/s towards north. The average acceleration of the body is.
View SolutionA body is moving with velocity 30m/s towards east. After 10s its velocity becomes 40m/s towards north. The average acceleration of the body is.
View SolutionThe velocity-time graph of an object is given below. Calculate the average acceleration of the object in the time interval of 4 s to 6 s.

View SolutionA boy standing at the top of a tower of 20m. Height drops a stone. Assuming g=10ms−2 towards north. The average acceleration of the body is.
View SolutionA body moves from rest with a uniform acceleration and travels 270 m in 3 s. Find the velocity of the body at 10 s after the start.
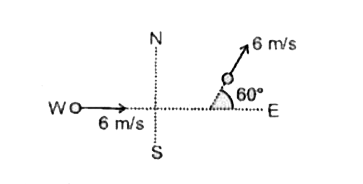
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
View SolutionFig. 2.38 shows the displacement of a body at different times.
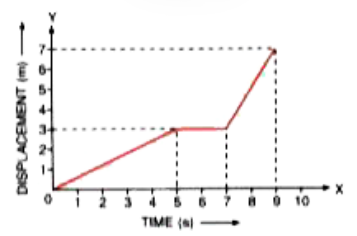
(a) Calculate the velocity of the body as it moves for time interval (i) 0 to 5 s,
(ii) 5 s to 7 S and
(iii) 7 s to 9 s.
(b) Calculate the average velocity during the time interval 5 s to 9 s. [Hint : From 5 s to 9 s, displacement = 7 m - 3 m = 4 m ]
View SolutionA body of mass m1 moving with a velocity 3m/s collides with another body at rest of m2 . After collision the velocities of the two bodies are 2m/s and 5m/s , respectively , along the direction of motion of m1. The ratio m1/m2 is
View Solution
