If length of the tangent is 12 cm and distance from circumference is 8 cm then radius will be
5 cm
13 cm
4 cm
12 cm
To find the radius of the circle given the length of the tangent and the distance from the circumference, we can follow these steps:
Step 1: Understand the problem
We are given:
- Length of the tangent (L) = 12 cm
- Distance from the circumference (d) = 8 cm
Step 2: Use the tangent-segment theorem
According to the tangent-segment theorem, the length of the tangent (L) from a point outside the circle to the point of tangency can be expressed in terms of the radius (r) and the distance from the center of the circle to the point where the tangent meets the line extended from the radius.
Step 3: Set up the equation
Let the radius of the circle be r. The distance from the center of the circle to the point where the tangent touches the circle is (r + d). Therefore, we can set up the equation using the Pythagorean theorem:
L2=(r+d)2−r2
Substituting the known values:
122=(r+8)2−r2
Step 4: Expand and simplify the equation
Expanding the equation gives:
144=(r2+16r+64)−r2
This simplifies to:
144=16r+64
Step 5: Solve for r
Now, isolate r:
144−64=16r
80=16r
r=8016=5
Final Answer
The radius of the circle is 5 cm.
---
We are given:
- Length of the tangent (L) = 12 cm
- Distance from the circumference (d) = 8 cm
According to the tangent-segment theorem, the length of the tangent (L) from a point outside the circle to the point of tangency can be expressed in terms of the radius (r) and the distance from the center of the circle to the point where the tangent meets the line extended from the radius.
Let the radius of the circle be r. The distance from the center of the circle to the point where the tangent touches the circle is (r + d). Therefore, we can set up the equation using the Pythagorean theorem:
Expanding the equation gives:
Now, isolate r:
80=16r
r=8016=5
The radius of the circle is 5 cm.
Similar Questions
A) The radius of a circle is 5 cm. At this point The tangent is drawn if the length of the tangent is 12 cm. Find the distance from the center of the circle to the point.
View SolutionFrom a point Q, the length of the tangent to a circle is 12 cm and distance of d from the centre is 13 cm. Find the radius of the circle.
View Solution
Knowledge Check
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
A7 cmB12 cmC15 cmD24.5 cmFrom a point Q, the length of the tangent to a circle is 12 cm and the distance of Q from the centre is 13 cm. The radius of the circle is 13 cm. The radius of the circle is :
A12 cmB13 cmC5 cmDNone of theseFrom an external point Q, the length of the tangents to a circle is 5 cm and the distance of Q from the centre is 8 cm. The radius of the circle is:
A39 cmB3 cmC√39 cmD7 cm
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
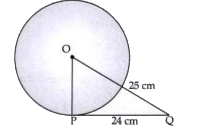
View SolutionFrom a point Q , the length of the tangent to a circle is 24cm and the distance of Q from the centre is 25cm. The radius of the circle is (a) 7cm (b) 12cm (c) 15cm (d) 24.5cm
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm, the radius of the circle is
View Solution
