In case of large or curved surface, flux can be found by
Integrating product E.△Sall over the surface
Integrating product E×△S all over the surface
by treating surface as plane surface and then flux ϕ=E.A
by using Coulomb’s law
The correct Answer is:A
To find the electric flux through a large or curved surface, we can follow these steps:
1. Understanding Electric Flux:
Electric flux (Φ) through a surface is defined as the number of electric field lines passing through that surface. It is mathematically represented as:
Φ=∫E⋅dS
where E is the electric field vector and dS is the differential area vector on the surface.
2. Choosing a Small Element:
For a large or curved surface, it is impractical to calculate the flux directly over the entire surface. Instead, we consider a small differential area dS on the surface.
3. Calculating the Dot Product:
For each small area element, we calculate the dot product E⋅dS. This gives us the contribution to the electric flux from that small area.
4. Integrating Over the Surface:
To find the total flux through the entire surface, we integrate the dot product over the entire surface area S:
Φ=∫SE⋅dS
This integral sums up the contributions from all the small area elements across the surface.
5. Final Result:
The final expression for the electric flux through a large or curved surface is given by the integral:
Φ=∫E⋅dS
This method is applicable for any surface, regardless of its shape, as long as the electric field is known.
Electric flux (Φ) through a surface is defined as the number of electric field lines passing through that surface. It is mathematically represented as:
Φ=∫E⋅dS
where E is the electric field vector and dS is the differential area vector on the surface.
For a large or curved surface, it is impractical to calculate the flux directly over the entire surface. Instead, we consider a small differential area dS on the surface.
For each small area element, we calculate the dot product E⋅dS. This gives us the contribution to the electric flux from that small area.
To find the total flux through the entire surface, we integrate the dot product over the entire surface area S:
Φ=∫SE⋅dS
This integral sums up the contributions from all the small area elements across the surface.
The final expression for the electric flux through a large or curved surface is given by the integral:
Φ=∫E⋅dS
This method is applicable for any surface, regardless of its shape, as long as the electric field is known.
Similar Questions
In each of the following cases, state whether you can draw line segments on the given surfaces: The face of a cuboid. The surface of an egg or apple. The curved surface of a cylinder. The curved surface of a cone. The base of a cone.
View SolutionAssertion:Although the surfaces of goggle lens are curved, It does not have any power.
Reason: In case of goggles, both the curved surfaces have equal radii of curvature and have centre of curvature on the same side.
View Solution
Knowledge Check
In case of eflection from curved surface
Athe normal is considered to be tangentto the spherical surface at the point of incidenceBthe normal is considered to be drawn at the polt of the spherical suface onlyCthe normal is the principle axis only.Dthe normal isnot required.Length of a curved surface can be measured by using
AprotractorBdividerCthreadDboth (b) and (c)Assertion : Although the surfaces of a goggle lens are curved, it does not have any power.
Reason: In case of goggles, both the curved surfaces have equal radii of curvature.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion and reason both are false.
Statement I: Although the surfaces of gogggle lengses are curved, it does not have any power.
Statement II: In case of goggle, both the curved surfaces have equal radii of curvature and have center of curvature on the same side.
View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in unit of voltmeter will be
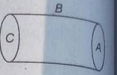
View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in unit of voltmeter will be

View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux is unit of volt -m associated with the curved surface B, the flux linked with the plane surface A in the same units will be

View SolutionA hollow cylinder has a charges q coulomb within it. If ϕ is the electric flux in units of V-m associated with the curved surface B, the flux linked with the plane surface A in units of V-m will be

View Solution
