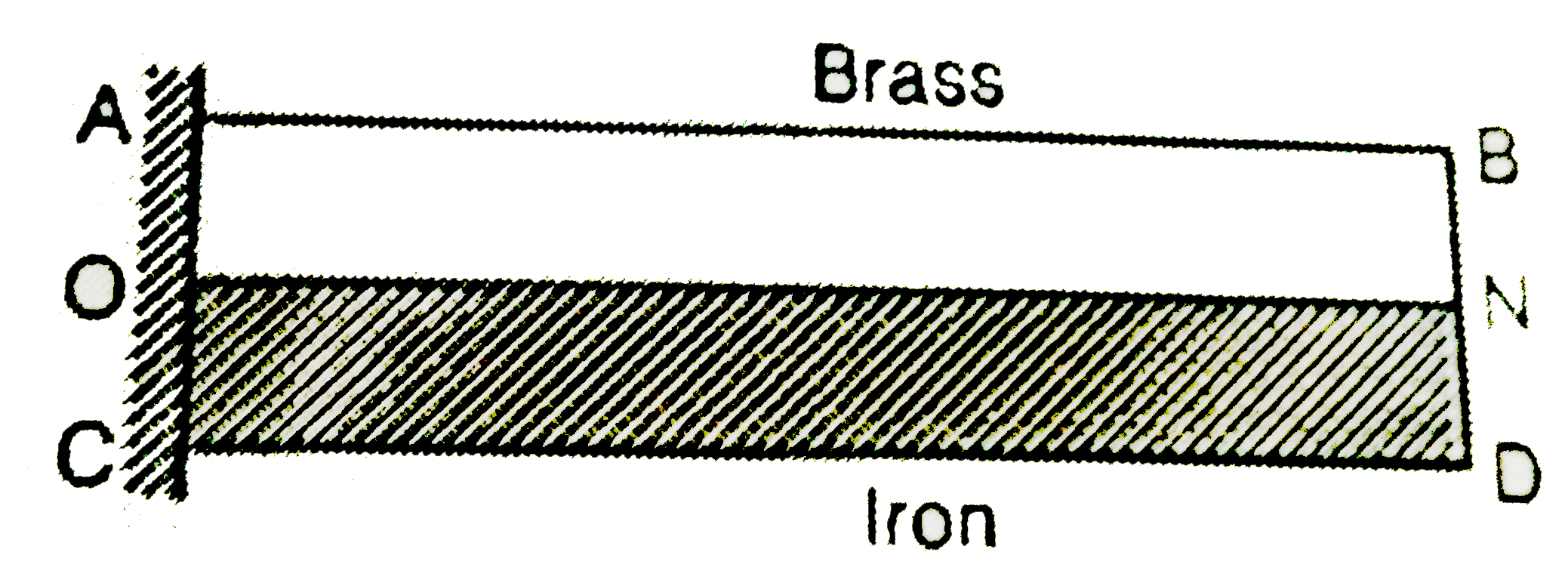
A bimetallic strip consists of brass and iron when it is heated it bends into an arc with brass on the convex and iron on the concave side of the arc. This happens, because
brass has a higher specific heat capacity than Iron
density of brass Is more than that of Iron
It Is easier to bend an iron strip than a brass strip of the same size
brass has a higher coefficient of linear expansion than Iron
The correct Answer is:D
To solve the question regarding the behavior of a bimetallic strip made of brass and iron when heated, we can follow these steps:
Step 1: Understand the concept of a bimetallic strip
A bimetallic strip consists of two different metals bonded together. When heated, these metals expand at different rates due to their differing coefficients of linear expansion.
Hint: Remember that different materials expand differently when heated.
Step 2: Identify the metals and their properties
In this case, we have brass and iron. Each metal has a specific coefficient of linear expansion, denoted as α (alpha). Let's denote the coefficient for brass as α₁ and for iron as α₂.
Hint: Coefficient of linear expansion indicates how much a material expands per degree of temperature change.
Step 3: Compare the coefficients of linear expansion
Brass has a higher coefficient of linear expansion (α₁) compared to iron (α₂). This means that when both metals are heated, brass will expand more than iron.
Hint: The metal with the higher coefficient will expand more when subjected to the same temperature increase.
Step 4: Analyze the bending of the strip
When the bimetallic strip is heated, the greater expansion of brass causes it to bend outward (convex side), while the lesser expansion of iron causes it to bend inward (concave side). Thus, the strip bends into an arc with brass on the convex side and iron on the concave side.
Hint: Visualize how unequal expansion leads to bending in one direction.
Step 5: Conclude the reason for bending
The bending occurs because brass has a higher coefficient of linear expansion than iron. Therefore, as the temperature increases, brass expands more significantly than iron, leading to the observed curvature of the strip.
Hint: The key takeaway is the relationship between thermal expansion and material properties.
Final Answer
The bimetallic strip bends into an arc with brass on the convex side and iron on the concave side because brass has a higher coefficient of linear expansion than iron.
A bimetallic strip consists of two different metals bonded together. When heated, these metals expand at different rates due to their differing coefficients of linear expansion.
In this case, we have brass and iron. Each metal has a specific coefficient of linear expansion, denoted as α (alpha). Let's denote the coefficient for brass as α₁ and for iron as α₂.
Brass has a higher coefficient of linear expansion (α₁) compared to iron (α₂). This means that when both metals are heated, brass will expand more than iron.
When the bimetallic strip is heated, the greater expansion of brass causes it to bend outward (convex side), while the lesser expansion of iron causes it to bend inward (concave side). Thus, the strip bends into an arc with brass on the convex side and iron on the concave side.
The bending occurs because brass has a higher coefficient of linear expansion than iron. Therefore, as the temperature increases, brass expands more significantly than iron, leading to the observed curvature of the strip.
The bimetallic strip bends into an arc with brass on the convex side and iron on the concave side because brass has a higher coefficient of linear expansion than iron.
Similar Questions
Knowledge Check
The strips of iron and zinc are riveted together to from a bimetallic strip which bends when heated . The iron is on the inside of the bend because
Ait has a higher coefficient of linear expansion .Bit has a lower coefficient of linear expansion .Cit has a higher specific heat .Dit has a lower specific heat .
Figure. Shows the graphs of elongation versus temperature for two different metals. If these metals are employed to form a straight bimetallic strip of thickness 6 cm and heated, it bends in the form of an arc, the radius of cuvature chaging with temperature approximately as shown in the figure. The linear expansivities of the two metals areA24×10−6/∘C and 12×10−6/∘CB20×10−6/∘C and 10×10−6/∘CC18×10−6/∘C and 9xx10^(-6)//^@CD16×10−6/∘C and 8×10−6/∘CA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficients of linear expansion of the strip goes up by ΔTand the strip bends to from an arc of radius of curvature R. Then R is.
Aproportional to ΔTBinversely proportional to ΔTCproportional to |αB−αC|Dinversely proportional to |αB−αC|
We would like to perpare a scale whose length does not change with temperature. It is proposed to prepare a unit scale f this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length (both components) would change in such a way that differnece between theri lenght rermain constant. If αiron=1.2×10−5/Kandαbrass=1.8×10−5/K, what should we take as lenght of each strip ?
View SolutionTwo straight thin bars, one of brass and the other of steel are joined togethre side by side by short steel cross-pieces at 0∘C, one cm long the centre lines of the bars being one cm apart. When heated to 100∘C, the composite bar becomes bent into the arc of a circle. calculate the radius of this circle.
α for brass =19×10−6 per .∘C
and α for steel =11×10−6 per .∘C
View SolutionA bimetallic strip is composed of two identical strips, one of steel and other of brass. When the temperature of the strip is raised by ΔT , it bends to form arc of curvature R. If the coefficients of linear expansion of steel and brass are α1 and α2 , respectively, then R is
View SolutionA bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
View SolutionTwo thin metal strips, one of brass and the other of iron are fastended together parallel to each other. Thickness of each strip is 2mm. If the strips are of equal length at 0∘C. The radius of the are formed by the bimetaalic strip when heated to 80∘C is (Coefficient of linear expansion of brass=19×10−6/∘C&
of iron=12×10−6/∘C).
View Solution