If the radius of gaussion surface increases, the electric flux is:
doubled
remains the same
halved
decreases
The correct Answer is:2
To solve the question regarding the effect of increasing the radius of a Gaussian surface on electric flux, we can follow these steps:
1. Understand Gauss's Law:
Gauss's Law states that the electric flux (Φ) through a closed surface is directly proportional to the charge (Q) enclosed within that surface. The mathematical expression of Gauss's Law is given by:
Φ=Qinϵ0
where Φ is the electric flux, Qin is the total charge enclosed by the Gaussian surface, and ϵ0 is the permittivity of free space.
Hint: Remember that Gauss's Law relates the electric flux to the charge enclosed, not the size of the surface.
2. Consider the Effect of Changing Radius:
When the radius of the Gaussian surface is increased, we need to consider whether this affects the charge enclosed. If the charges inside the Gaussian surface remain the same, then the enclosed charge Qin does not change.
Hint: Focus on whether the charges inside the Gaussian surface are changing or not.
3. Analyze the Situation:
- If the radius is increased, the Gaussian surface can encompass more area, but it does not mean that more charge is enclosed unless additional charges are introduced within that surface.
- The electric flux depends solely on the charge enclosed. If the enclosed charge remains constant, the electric flux will also remain constant.
Hint: Think about how the electric field behaves with respect to the charges inside the surface.
4. Conclusion:
Since the charge enclosed Qin remains the same when only the radius of the Gaussian surface is increased, the electric flux Φ also remains the same. Therefore, the correct answer to the question is that the electric flux remains the same.
Final Answer: The electric flux is B) remains the same.
Gauss's Law states that the electric flux (Φ) through a closed surface is directly proportional to the charge (Q) enclosed within that surface. The mathematical expression of Gauss's Law is given by:
Φ=Qinϵ0
where Φ is the electric flux, Qin is the total charge enclosed by the Gaussian surface, and ϵ0 is the permittivity of free space.
When the radius of the Gaussian surface is increased, we need to consider whether this affects the charge enclosed. If the charges inside the Gaussian surface remain the same, then the enclosed charge Qin does not change.
- If the radius is increased, the Gaussian surface can encompass more area, but it does not mean that more charge is enclosed unless additional charges are introduced within that surface.
- The electric flux depends solely on the charge enclosed. If the enclosed charge remains constant, the electric flux will also remain constant.
Since the charge enclosed Qin remains the same when only the radius of the Gaussian surface is increased, the electric flux Φ also remains the same. Therefore, the correct answer to the question is that the electric flux remains the same.
Topper's Solved these Questions
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - B
22 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER SELF- ASSESSMENT -(10)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF- ASSESSMENT -(10)EXERCISE - SECTION-B
17 Videos
Similar Questions
A spherical Gaussian surface encloses a charge of 8.85×10−8C (i) Calculate the electric flux passing through the surface (ii) If the radius of Gaussian surface is doubled, how would the flux change ?
View SolutionIf the radius of the Gaussion surface enclosing a charge q is halved, how does the electric flux through the Gaussion surface change?
View Solution
Knowledge Check
If the size of the gaussian surface increases, the flux through the body:
AdecreasesBIncreasesCremains the sameDfluctuatesA point charge causes an electric flux of −200Nm2/C to pass through spherical Guassian surface of 10 cm radius centered on the charge. If the radius of the Guassian surface is doubled, the total electric flux passing through the surface is
A−200Nm2/CB−100Nm2/CC+200Nm2/CD−50Nm2/CFigure shows. In cross section m three solid cylinders, each of length L and uniform charge Q. Concentric with each cylinder is a cylindrical Gaussian surface, with all three surfaces having the same radius. Rank the Gaussian surface according to the electric field at any point on the surface, greatest first.
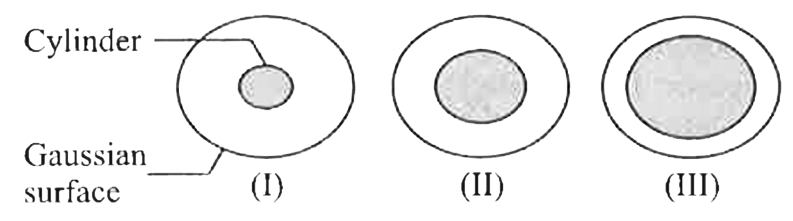 AI→II→IIIBII→I→IIICIII→II→IDall tie
AI→II→IIIBII→I→IIICIII→II→IDall tie
" A change of "8.85C" is placed at the centre of a spherical Guassion surface of radius "5cm" .The electric flux through the surface "
View SolutionA charge of 8.85C is placed at the centre of a spherical Gaussian surface of radius 5cm .The electric flux through the surface ..
View SolutionA point charges causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charges.
If the radius of the Gaussian surface were doubled , how much flux would pass through the surface?
What is the value of the point charges?
View SolutionDefine electric flux. Write its SI unit. A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change ?
View SolutionA charge of 5C is placed at the curve of a spherical gaussian of radius 5cm the electric flux through the surface is 1ε0 times of
View Solution
