In the adjoining figure, DE is parallel to BC and AD=1cm , BD=2cm . What is the ratio of the area of ABC to the area of ADE ?
The correct Answer is:9:1
Step by step video, text & image solution for In the adjoining figure, D E is parallel to B C and A D=1c m , B D=2c m . What is the ratio of the area of A B C to the area of A D E ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-II) TYPE QUESTIONS
21 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - VERY SHORT QUESTIONS
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos
Similar Questions
In Figure, ABCD is a rectangle in which CD=6cm,AD=8cm Find the area of parallelogram CDEF

View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG

View SolutionABCD is a square. E is the mid-point of BC and F is the mid-point of CD . The ratio of the area of triangle AEF to the area of the square ABCD is (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 3 : 8
View SolutionIn Fig. 4.178, DEBC (FIGURE) If DE=4cm , BC=6cm and Area (ADE)=16 cm2 , find the area of ABC . (ii) If DE=4cm, BC=8cm and Area (ADE)=25 cm2 , find the area of ABC . (iii) If DE:BC=3:5 . Calculate the ratio of the areas of ADE and the trapezium BCED .
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
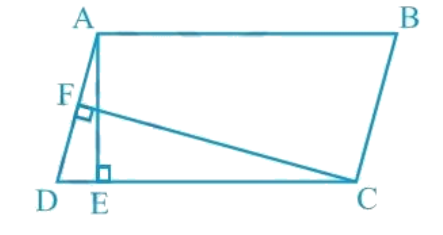
View SolutionIn Fig. 21, ABCD is a parallelogram, DL⊥AB. If AB=20 cm , AD=13 cm and area of the parallelogram is 100 cm2 find AL.
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View SolutionIn fig. AB,DEandGF are parallel to each other and AD,BGandEF are parallel to each other. If CD:CE=CG:CB=2:1, then the value of area (AEG): area (ABD) is equal to 7/2 b. 3 c. 4 d. 9/2
View Solution
