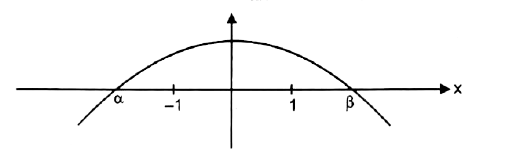
Which of the following condition is correct for the graph of quadratic polynomial p(x) = ax2+bx+c to be an upward parabola?
a<0
a=0
a>0
b=0
The correct Answer is:C
To determine the condition for the graph of the quadratic polynomial p(x)=ax2+bx+c to be an upward-opening parabola, we can follow these steps:
1. Identify the standard form of a quadratic polynomial:
The standard form of a quadratic polynomial is given by:
p(x)=ax2+bx+c
where a, b, and c are real numbers and a≠0.
Hint: Recall that the term ax2 determines the shape of the parabola.
2. Understand the role of the coefficient a:
The coefficient a in the quadratic polynomial plays a crucial role in determining the direction in which the parabola opens.
Hint: Think about how positive and negative values of a affect the graph.
3. Determine the condition for an upward-opening parabola:
- If a>0 (i.e., the coefficient of x2 is positive), the parabola opens upwards.
- If a<0 (i.e., the coefficient of x2 is negative), the parabola opens downwards.
Hint: Visualize the graph of a parabola with different values of a.
4. Conclusion:
Therefore, for the graph of the quadratic polynomial p(x)=ax2+bx+c to be an upward-opening parabola, the condition is:
a>0
Final Answer: The correct condition is that a should be positive.
The standard form of a quadratic polynomial is given by:
p(x)=ax2+bx+c
where a, b, and c are real numbers and a≠0.
The coefficient a in the quadratic polynomial plays a crucial role in determining the direction in which the parabola opens.
- If a>0 (i.e., the coefficient of x2 is positive), the parabola opens upwards.
- If a<0 (i.e., the coefficient of x2 is negative), the parabola opens downwards.
Therefore, for the graph of the quadratic polynomial p(x)=ax2+bx+c to be an upward-opening parabola, the condition is:
a>0
Topper's Solved these Questions
- SAMPLE PAPER 4BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - SECTION - B
20 Videos
- SAMPLE PAPER 4BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - SECTION - C
10 Videos
- SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]EXERCISE - SECTION - D
12 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - B (SECTION - V)
4 Videos
Similar Questions
Knowledge Check
Which of the following condition is correct for the graph of a quadratic polynomial p(x) = ax2+bx+c to be an upward parabola?
Aa<0Ba=0Ca>0Db=0Which of the following is not the graph of a quadratic polynomial?
A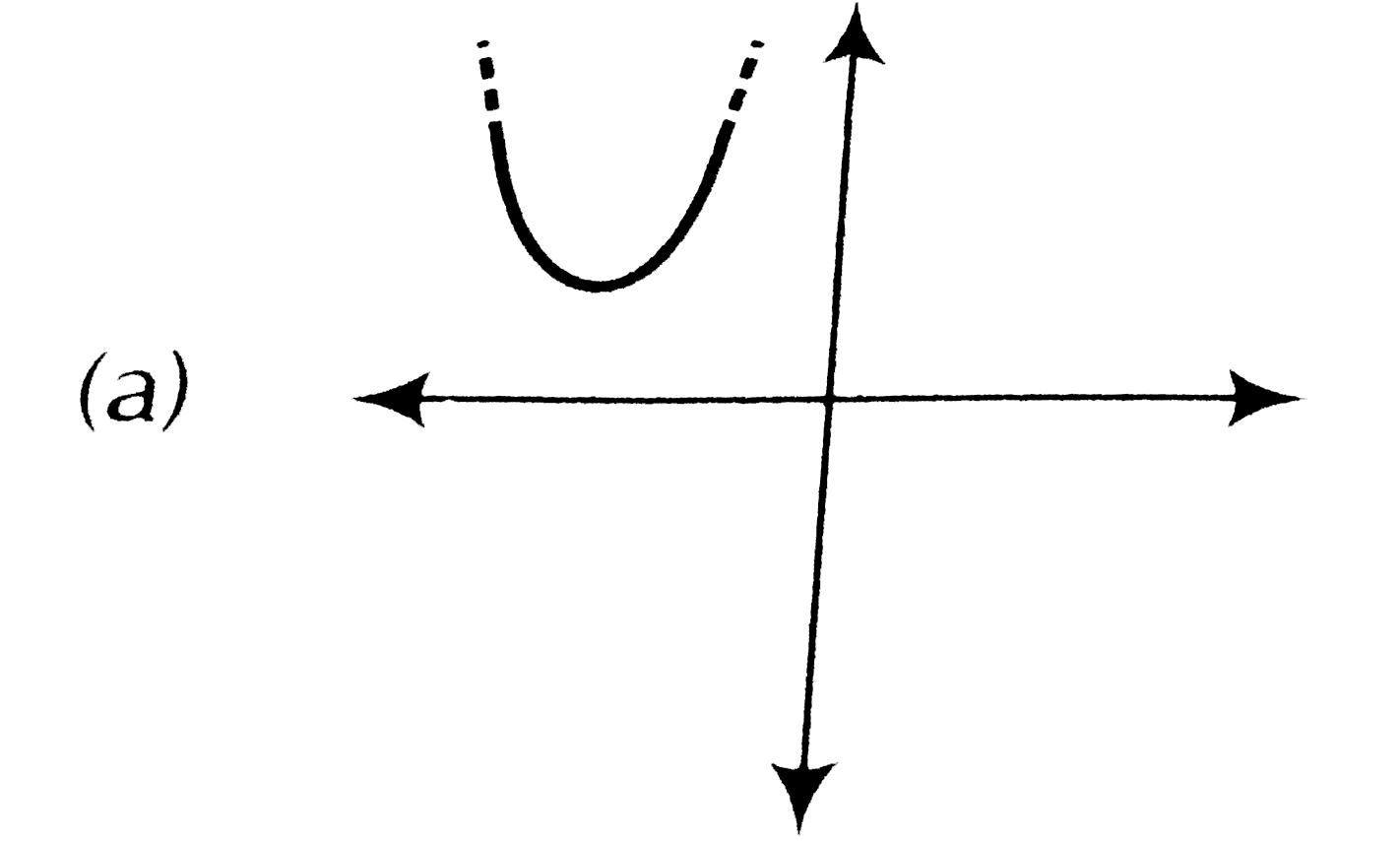 B
B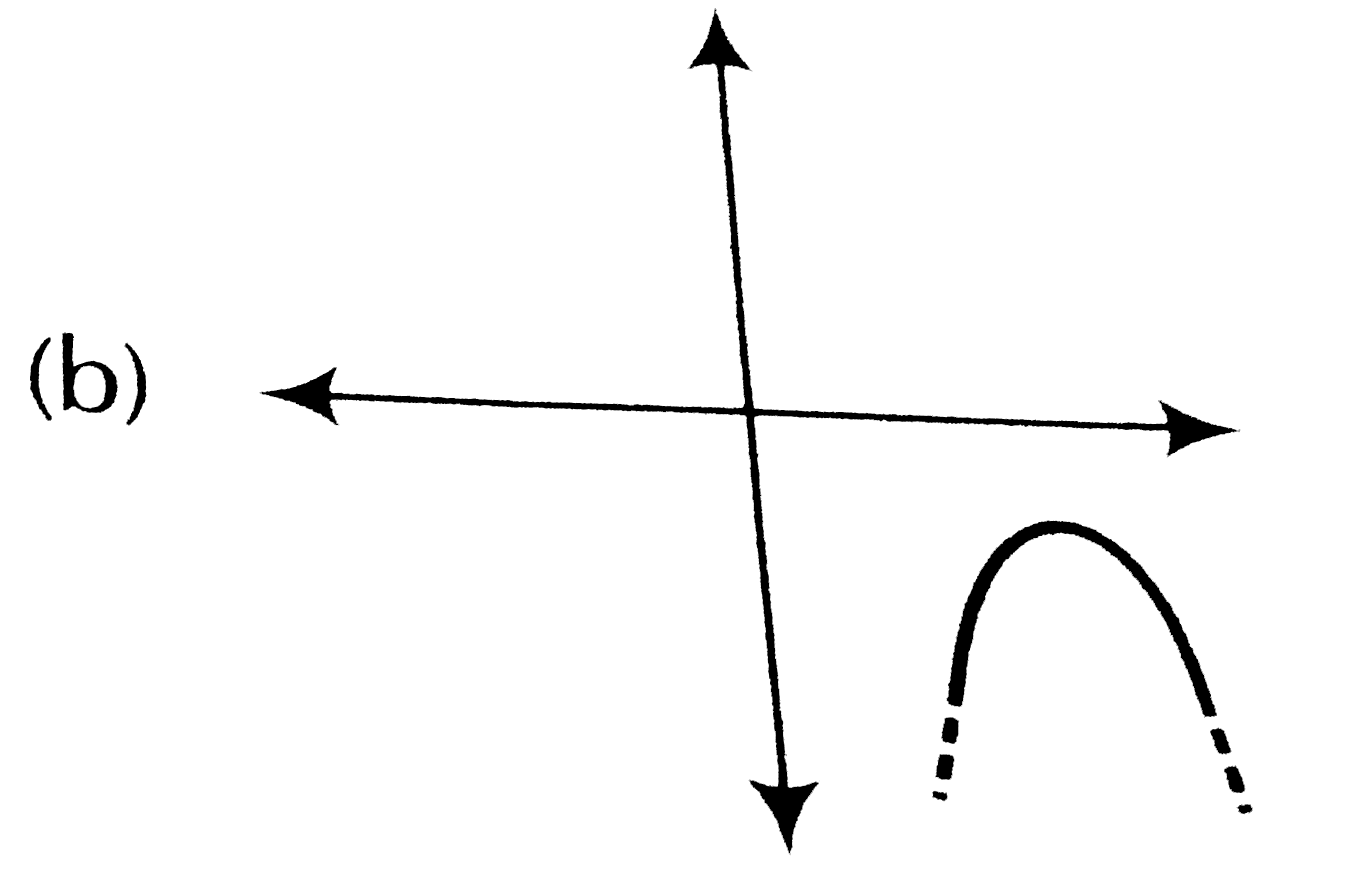 C
C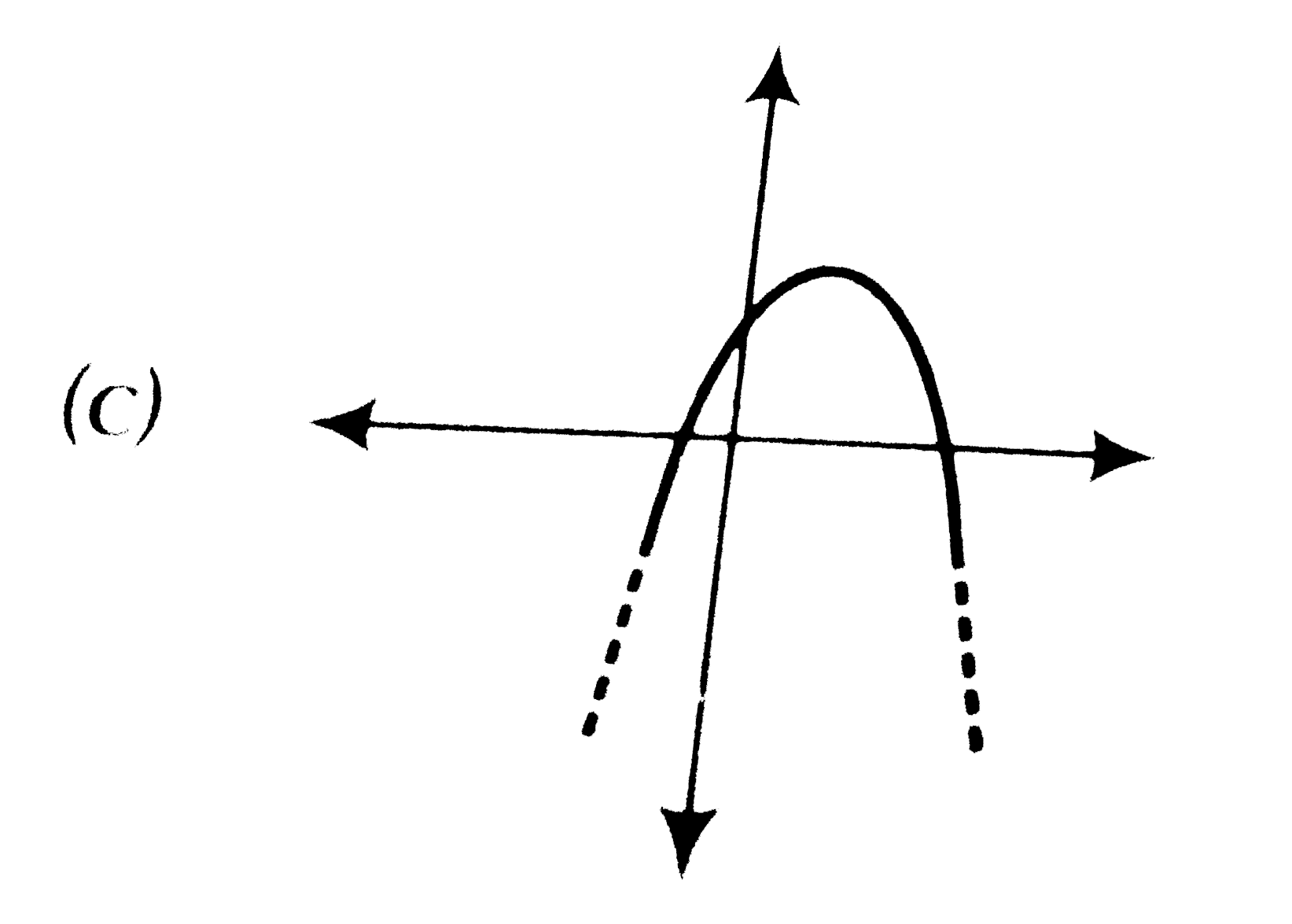 D
D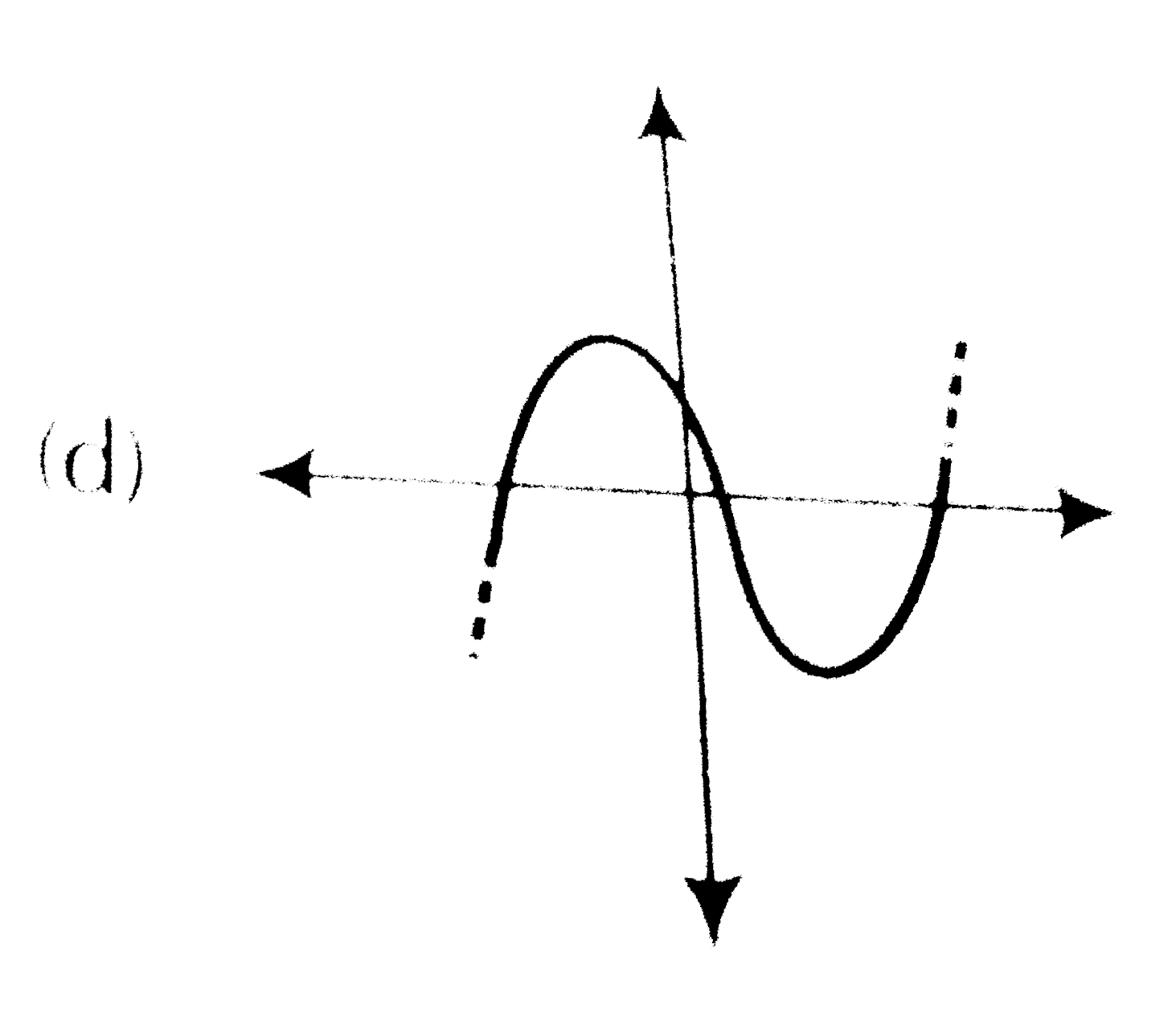
If the zeroes of the quadratic polynomial ax2+bx+c,c≠0 are equal,then
Ac and a have opposite signsBc and b have opposite signsCc and a have the same signDc and b have the same sign
Which of the following is not the graph of a quadratic polynomial?
View SolutionFind the sum and product of zeros of the quadratic polynomial ax2+bx+c.
View SolutionFactorization of quadratic polynomials of theorem ax2+bx+c and a≠1
View Solution.
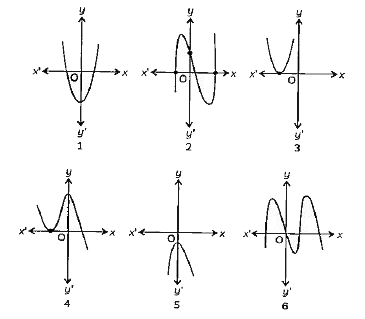
Which of the above graph represent quadratic polynomials?
View SolutionThe graph of the quadratic polynomial y=ax2+bx+c is as shown in the figure.Then
View Solution