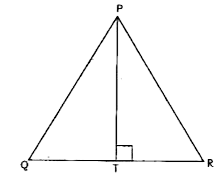
In an equilateral triangle $Δ P Q R, P T$ is an altitude. Then the value of $4 P T^{2}$ is:

$3 P Q^{2}$

${(P Q + Q R)}^{2}$

$P Q^{2}$

$2 P Q^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for In an equilateral triangle DeltaPQR, PT is an altitude. Then the value of 4PT^(2) is: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

In an equilateral triangle of side 2a, calculate the length of its altitude.
A $2 a \sqrt{3}$
B $a \sqrt{3}$
C $a \frac{\sqrt{3}}{2}$
Dnone of these
$A B C$ is an equilateral triangle of side $2 a$ . Find each of its altitudes.
A $a \sqrt{3}$
B $a \sqrt{2}$
C $2 a \sqrt{3}$
DNone
If each side of an equilateral triangle is 12 cm, then its altitude is equal to:
A $6 \sqrt{2} c m$
B $3 \sqrt{2}$ cm
C $6 \sqrt{3} c m$
D $3 \sqrt{6}$ cm

EDUCART PUBLICATION-SAMPLE PAPER 02-SECTION-B

Home
Ask Doubt
Profile

In an equilateral triangle ΔPQR,PT is an altitude. Then the value of 4PT2 is:

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

In an equilateral triangle of side 2a, calculate the length of its altitude.

ABC is an equilateral triangle of side 2a. Find each of its altitudes.

If each side of an equilateral triangle is 12 cm, then its altitude is equal to:

EDUCART PUBLICATION-SAMPLE PAPER 02-SECTION-B

In an equilateral triangle $Δ P Q R, P T$ is an altitude. Then the value of $4 P T^{2}$ is:

$A B C$ is an equilateral triangle of side $2 a$ . Find each of its altitudes.