Question

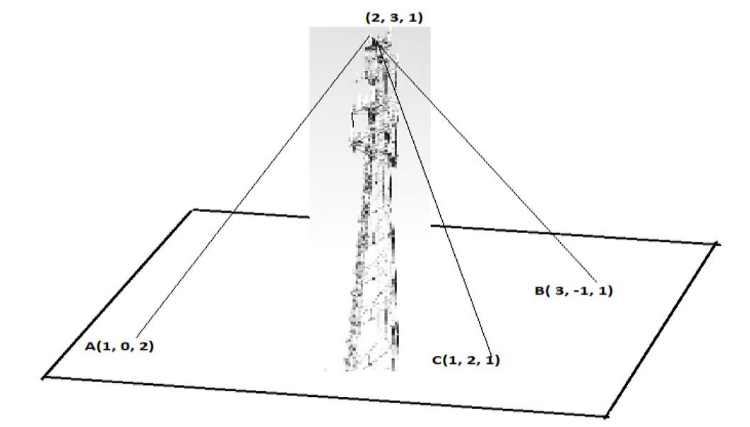
A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, -1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the point A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

Based on the above answer the following:
The equation of the plane passing through the points A, B and C is

Options

A. `(x - 1)/(2) = (y + 3)/(1) = (z-5)/(-2)`
B. `(x - 2)/(-3) = (y - 3)/(2) = (z - 1)/(4)`
C. `(x - 2)/(3) = (y - 3)/(2) = (z - 1)/(4)`
D. `(x + 1)/(-2) = (y + 3)/(-1) = (z - 5)/(2)`

Answer

C