The difference between the radii of the bigger circle and smaller circle is 14 cm and the difference between their areas is 1056cm2. Radius of the smaller circle is
7 cm
5 cm
9 cm
3 cm
The correct Answer is:B
πx2−π(x−14)2=1056
⇒x2−x2−196+28x=1056×722
⇒28x=336+196
⇒x=53228=19
∴ छोटे वृत्त की त्रिज्या=19-14=5cm
Similar Questions
Find the ratio of the area of the bigger circle and smaller circle.
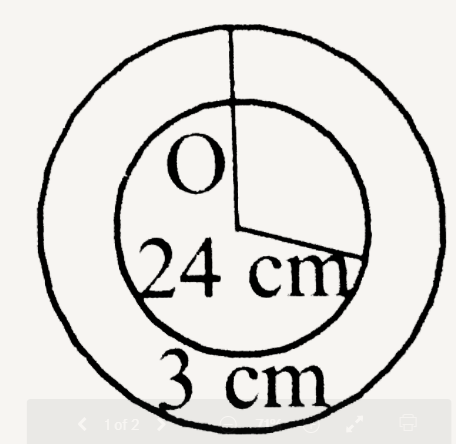
I. The radius of the smaller circle is 24 cm.
II. The difference between the radii of bigger and the smaller circles is 3 cm.
View SolutionThe difference between the circumference and radius of a circle is 37 cm. Find the area of the circle
View Solution
Knowledge Check
The difference between the radii of the smaller circle and the bigger circle is 7 cm and the difference between the areas of the two circles is 1078 sq cm. What is the radius of the smaller circle in cm?
A28B21C17.5D35The sum of the radii of the two circle is 140 cm and the difference between their circumference is 88 cm. The radius of the larger circle is :
A60 cmB70 cmC63 cmD77 cmThe sum of the radii of the two circle is 140 cm and the difference between their circumference is 88 cm. The radius of the larger circle is :
A60 cmB70 cmC63 cmD77 cm
The difference between the area of circle and square of radius r is 105 cm^2. What will be the circumference of the circle?
View SolutionThe differences between the circumference and diameter of a circle is 60 cm, then radius is
View SolutionTwo circles touch each externally. The sum of their areas is 130π sq cm and the distance between their centres is 14 cm. The radius of the smaller circle is
View SolutionTwo circles touch each other externally. The distance between their centres is 8 cm. If the radius of one circle is 3 cm, then the radius of the other circle is:
दो वृत्त एक दूसरे को बाह्य रूप से स्पर्श करते हैं। उनके केंद्रों के बीच की दूरी 8 सेमी है। यदि एक वृत्त की त्रिज्या 3 सेमी है, तो दूसरे वृत्त की त्रिज्या है:
View SolutionThe difference between the circumference and radius of a circle is 37 cm. The area of the circle is
View Solution
