माना विद्युत चुम्बकीय तरंग के विद्युत क्षेत्र का आयाम E0=120न्यूटन कूलॉम−1 और इसकी आवृत्ति ν=50 मेगा-हर्ट्स है, तब E का समीकरण होगा (यदि तरंग X-दिशा में गमन करती हो) 1)[(120NC−1)sin[(1.05radm−1)x−(3.14×108rads−1)t]ˆi 2)[(120NC−1)sin[(1.05radm−1)x−(3.14×108rads−1)t]ˆi 3)[(120NC−1)sin[(1.05radm−1)x−(3.14×108rads−1)t]ˆj 4)[(120NC−1)cos[(1.05radm−1)x−(3.14×108rads−1)t]ˆj
[(120NC−1)sin[(1.05radm−1)x−(3.14×108rads−1)t]ˆi
[(120NC−1)sin[(1.05radm−1)x−(3.14×108rads−1)t]ˆi
[(120NC−1)sin[(1.05radm−1)x−(3.14×108rads−1)t]ˆj
[(120NC−1)cos[(1.05radm−1)x−(3.14×108rads−1)t]ˆj
The correct Answer is:C
दिया गया है, E0=120 न्यूटन कूलॉम.−1
ν=50 मेगा हर्ट्ज
=50×106 हर्ट्ज
हम जानते हैं, चुम्बकीय क्षेत्र,
B0=E0c=1203×108=4×10−7 टेस्ला =400 नैनो टेस्ला
ω−2πν=(2×3.14)(50×106)=3.14×108 रेडियन से−1
तरंग नियतांक,k=ωc=3.14×1083×108=1.05रेडियन मी−1
तरंगदैर्य, λ=cν=3×10850×106=6.00 मीटर
यदि तरंग X-अक्ष के अनुदिश संचरित होती है, तब E व B क्रमश: Y-अक्ष एवं 2-अक्ष के अनुदिश संचरित होगें।
E=E0sin(kx−ωt)ˆj
=(120)sin{(1.05)x−(3.14×108)t}]ˆj
Topper's Solved these Questions
- विद्युत चुम्बकीय तरंगे BOOK - NEET PREVIOUS YEARCHAPTER - विद्युत चुम्बकीय तरंगे EXERCISE - NCERT पर based Objective प्रश्न(टॉपिक 4 विद्युत चुम्बकीय स्पेक्ट्रम)
18 Videos
- विद्युत चुम्बकीय तरंगे BOOK - NEET PREVIOUS YEARCHAPTER - विद्युत चुम्बकीय तरंगे EXERCISE - Special Format वाले Objective प्रश्न(I. कथन-कारण)
4 Videos
- विद्युत चुम्बकीय तरंगे BOOK - NEET PREVIOUS YEARCHAPTER - विद्युत चुम्बकीय तरंगे EXERCISE - NCERT पर based Objective प्रश्न(टॉपिक 2 मैक्सवेल के समीकरण)
8 Videos
- विद्युत आवेश तथा क्षेत्र BOOK - NEET PREVIOUS YEARCHAPTER - विद्युत आवेश तथा क्षेत्र EXERCISE - बहुविकल्पीय प्रश्न
38 Videos
- विद्युत चुम्बकीय प्रेरणाBOOK - NEET PREVIOUS YEARCHAPTER - विद्युत चुम्बकीय प्रेरणाEXERCISE - NCERT व NCERT Exemplar के प्रश्न(NCERT Exemplar)
10 Videos
Similar Questions
जिस समय मैक्सवेल ने विद्युत चुम्बकीय तरंगों की उपस्थिति का अनुमान लगाया, उस समय बहुत ही परिचित विद्युत चुम्बकीय तरंग निम्न में से कौन-सी थी?
View Solutionकथन समान परिधि के दिए गए सतहों के लिए ऐम्पियर के परिपथीय नियम का प्रयोग करते समय ∮B.dl=μ0i(t) बाई दिशा में परिवर्तित नहीं होता है, लेकिन दाई दिशा से शून्य होता है।
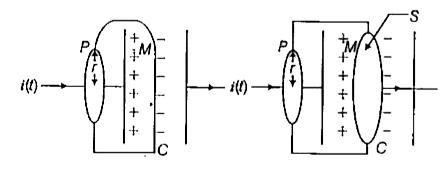
कारण सतह से कोई धारा प्रवाहित नहीं होती है।
View Solutionनिम्न में से मैक्सवेल के समीकरण को प्रकट करने के लिए सबसे महत्वपूर्ण पर्व कथन कौन-सा है?
View Solutionबिन्दु आवेश + 4q, -qतथा +4q,x-अक्ष के बिन्दु x =0,x=a,x= 2a पर रखे गये हैं।
View SolutionL मीटर भुजा वाला एक वर्ग xy-समतल में ऐसे क्षेत्र में रखा है जहाँ चुम्बकीय क्षेत्र B=B0(2ˆi+3ˆk+4ˆk) टेस्ला है, जहाँ B0 नियतांक है। वर्ग से गुजरने वाला चुम्बकीय फ्लक्स का परिमाण है
View Solution(x ^ (3) sin (tan ^ (- 1) x ^ (4))) / (1 + x ^ (8))
View SolutionThe angle made by the tangent of the curve x=a(t+sintcost),y=a(1+sint)2 with the x-axis at any point on it is (A)14(π+2t) (B) 1−sintcost (C) 14(2t−π) (D) 1+sintcos2t
View SolutionThe the term independent in the expansion of [(t^(-1)-1)x+(t^(-1)+1)^(-1)x^(-1)]^(8) is
View Solutionsin ^ (8) x-cos ^ (8) x = 1
View Solutionx3sin(tan−1x4)1+x8
View Solutionlimx→1⎛⎝∫(x−1)0tcos(t)dt(x−1)sin(x−1)⎞⎠
View SolutionIf ∫1sinxt2f(t)dt=1−sinx, then the value of f(1√3) is :
View SolutionFind the value of x if sin−1(18)=cos−1x
View SolutionThe term independent of x in the expansion of
(x2−1x)6 is
View SolutionFind the term independent of x in the expansion of [(t−1−1)x+(t−1+1)−1x−1]8
View SolutionThe the term independent in the expansion of [(t−1−1)x+(t−1+1)−1x−1]8 is
View Solution
