Read the data given below and answer the questions based on it.
There were 3 sections namely A, B and C in a test. Out of three 33 students passed in section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each section alone was equal and was 21 for each section.
The ratio of the number of students passed in one or more of the sections to the number of students who passed in section A alone is :
A. 78/21
B. 3
C. 73/21
D. 75/21
B
D
C
A
The correct Answer is:D
To solve the problem step by step, we will use a Venn diagram approach to visualize the distribution of students across the three sections (A, B, and C).
Step 1: Set Up the Venn Diagram
We have three sections: A, B, and C. We know the following:
- 33 students passed in Section A.
- 34 students passed in Section B.
- 32 students passed in Section C.
- 10 students passed in both A and B.
- 9 students passed in both B and C.
- 8 students passed in both A and C.
- 21 students passed each section alone.
Step 2: Define Variables
Let:
- x = number of students who passed all three sections (A, B, and C).
Step 3: Fill in the Venn Diagram
From the information provided:
- Students who passed only A = 21
- Students who passed only B = 21
- Students who passed only C = 21
Now, we can express the number of students who passed in combinations:
- Students who passed A and B only = 10−x
- Students who passed B and C only = 9−x
- Students who passed A and C only = 8−x
Step 4: Set Up Equations
Now we can set up equations based on the total number of students who passed in each section:
1. For Section A:
21+(10−x)+(8−x)+x=33
Simplifying this:
21+10−x+8−x+x=33⟹39−x=33⟹x=6
2. For Section B:
21+(10−x)+(9−x)+x=34
Substituting x=6:
21+(10−6)+(9−6)+6=34⟹21+4+3+6=34 (This holds true)
3. For Section C:
21+(8−x)+(9−x)+x=32
Substituting x=6:
21+(8−6)+(9−6)+6=32⟹21+2+3+6=32 (This holds true)
Step 5: Calculate Total Students Who Passed in One or More Sections
Now, we need to calculate the total number of students who passed in one or more sections:
- Students who passed only A = 21
- Students who passed only B = 21
- Students who passed only C = 21
- Students who passed A and B only = 10−6=4
- Students who passed B and C only = 9−6=3
- Students who passed A and C only = 8−6=2
- Students who passed all three = 6
Adding these together:
21+21+21+4+3+2+6=78
Step 6: Calculate the Ratio
The ratio of the number of students who passed in one or more sections to the number of students who passed in section A alone is:
Ratio=7821
Final Answer
Thus, the answer is 7821.
We have three sections: A, B, and C. We know the following:
- 33 students passed in Section A.
- 34 students passed in Section B.
- 32 students passed in Section C.
- 10 students passed in both A and B.
- 9 students passed in both B and C.
- 8 students passed in both A and C.
- 21 students passed each section alone.
Let:
- x = number of students who passed all three sections (A, B, and C).
From the information provided:
- Students who passed only A = 21
- Students who passed only B = 21
- Students who passed only C = 21
- Students who passed A and B only = 10−x
- Students who passed B and C only = 9−x
- Students who passed A and C only = 8−x
Now we can set up equations based on the total number of students who passed in each section:
21+(10−x)+(8−x)+x=33
Simplifying this:
21+10−x+8−x+x=33⟹39−x=33⟹x=6
21+(10−x)+(9−x)+x=34
Substituting x=6:
21+(10−6)+(9−6)+6=34⟹21+4+3+6=34 (This holds true)
21+(8−x)+(9−x)+x=32
Substituting x=6:
21+(8−6)+(9−6)+6=32⟹21+2+3+6=32 (This holds true)
Now, we need to calculate the total number of students who passed in one or more sections:
- Students who passed only A = 21
- Students who passed only B = 21
- Students who passed only C = 21
- Students who passed A and B only = 10−6=4
- Students who passed B and C only = 9−6=3
- Students who passed A and C only = 8−6=2
- Students who passed all three = 6
21+21+21+4+3+2+6=78
The ratio of the number of students who passed in one or more sections to the number of students who passed in section A alone is:
Ratio=7821
Thus, the answer is 7821.
Similar Questions
The pie chart given below shows the number of students in 6 different sections. The total number of students is 1800.
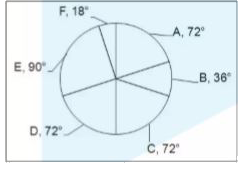
What is the ratio of number of students in section D to the number of students in section F and B?
View SolutionThe pie chart given below shows the number of students in 6 different sections. The total number of students is 1800.
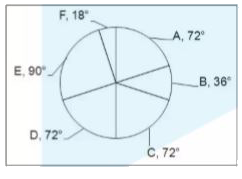
What is the difference between the number of students in section F to the number of students in section C?
View Solution
Knowledge Check
Read the data given below and answer the quesitons based on it.
There were 3 sections namely A, B and C in a test. Out of three sections, 33 passed section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each seciton alone was equal and was 21 for each section.
How many passed all the three sections ?
A. 3
B. 6
C. 5
D. 7ABBACCDDDirection: Read the data given below and answer the question based on it. There were 3 sections namely A, B and C in a test. Out of three sections, 33 students passed in Section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each section alone was equal and was 21 for each section.How many passed only one of the three sections ?
A. 21
B. 42
C. 63
D. 52AABCCDDBIn a school, the number of students in each section is equal to the number of sections. If the total number of students is 625, then find the numbr of sections
A10B20C15D25
The average marks of section A are 65 and that of section B are 70. If th average marks of both the sections combined are 67, then the ratio of the number of studnts of section A to that of section B is
View SolutionThe pie chart given below sows the number of students in 6 different sections. The total number of students is 1800.
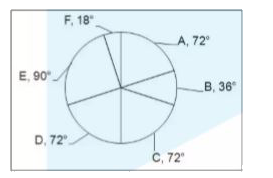
What is the average number of students in section A, B and F?
View SolutionThe table given below shows the number of students adimitted in 2 sections X and Y from year 2011 to 2015.
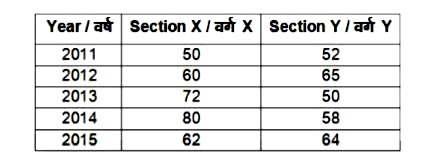
In year 2012, the number of students admitted in section Y is what percent of that of the number of students admitted in section X?
View SolutionThe pie chart given below shows the number of students in 5 sections .The number of students is 7200.
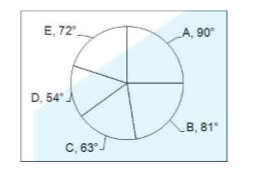
What is the total number of students in section E and section B?
View SolutionThe line chart given below shows the number of students in 2 sections X and Y from year 2009 to 2016.
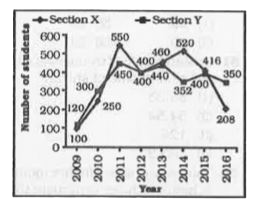
For how many years was the number of students in section Y was more than that of section X?
View Solution
