For a particle in uniform motion the acceleration a at a point p on the circle of radius r is (here is measured from the x-axis )
The correct Answer is:C
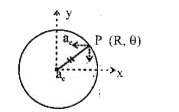
For a particle in uniform circular motion .
towards centre of circle ,
Similar Questions
For a particle in uniform circular motion, the acceleration →a at a point P(R,θ) on the circle of radius R (Here is measured from the x-axis) is
View SolutionFor a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
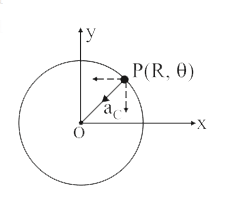
View Solution
Knowledge Check
For a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
 A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2Rˆj
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2RˆjFor a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθˆi−v2RsinθˆjD−v2Rˆi+v2RˆjThe area of a sector of angle θ∘ of a circle with radius R is
A2πRθ180BπR2θ180C2πRθ360DπR2θ360
For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
View SolutionFor a particle in uniform circular motion the acceleration a at a point P(R,θ) on the circle of radius R is (here 'v' is the speed of the particle and θ is measured from the x-axis)
View SolutionThe acceleration of an object moving in a circle of radius R with uniform speed v is
View SolutionWrite the formula for the area of a sector of angle θ (in degrees) of a circle of radius r .
View SolutionThe acceleration of an object moving in a circle of radius R with uniform speed v is
View Solution

