Obtain the expression for electric field due to an uniformly charge spherical shell. Solution in Tamil
Electric field due to a uniformly charged spherical shell :
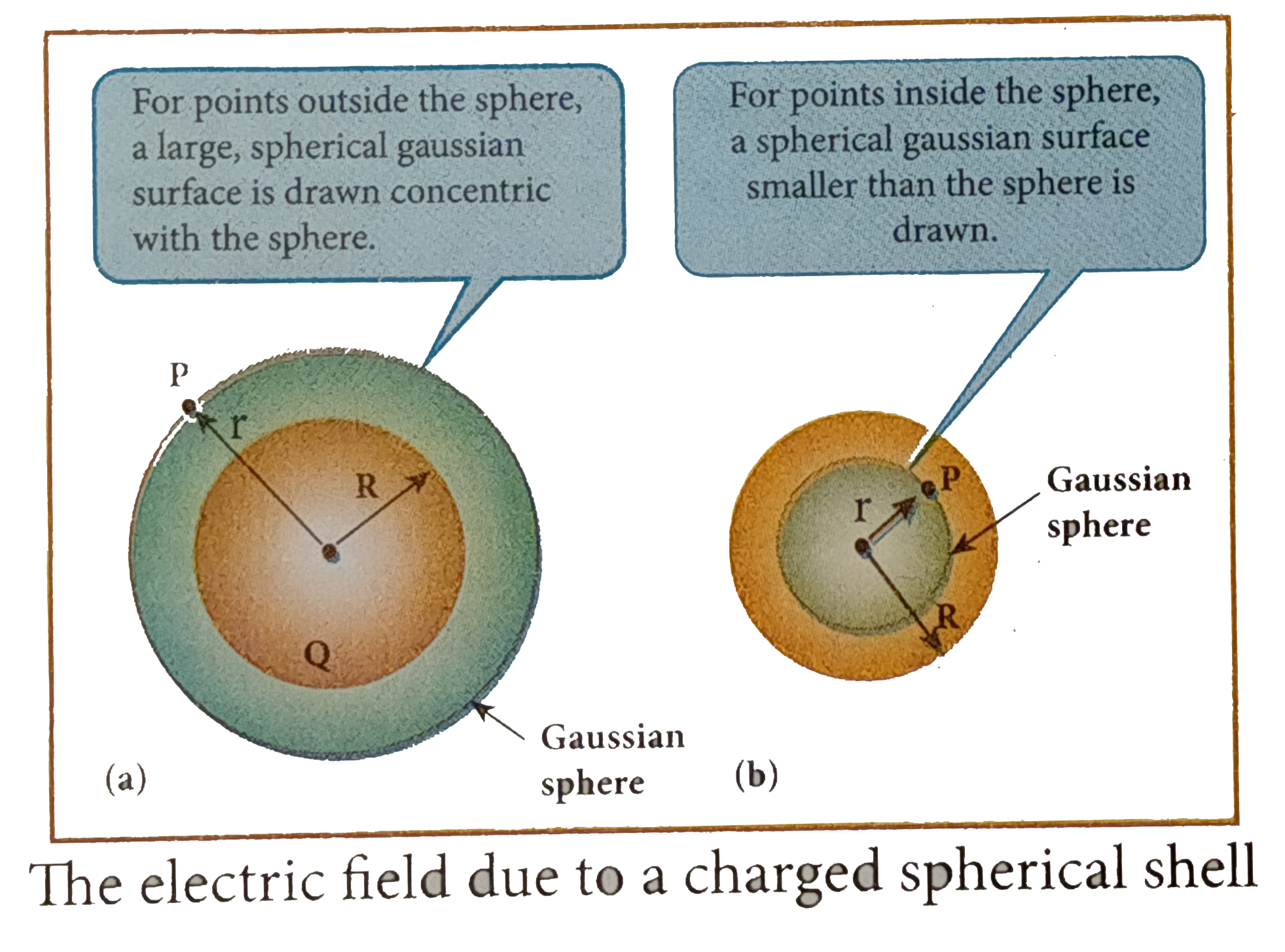
Consider a uniformly charged spherical shell of radius R and total charge Q as shown in Figure 1.42. The electric field at points outside and inside the sphere is found using Gauss law.
Case (a) At a point outside the shell (r>R) (i) A point P outside the shell at a distance r from the center as shown in Figure (a). The charge is uniformly distributed on the surface of the sphere (spherical symmetry). Hence the electric field must point radially outward if Q>0 and point radially inward if Q<0.
(ii) A spherical Gaussian surface of radius r is chosen and the total charge enclosed by this Gaussian surface is Q. Applying Gauss law
∮Gaussion surface→E.d→A=Qε0 .........(1)
(iii) The electric field →Eandd→A point in the same direction (outward normal) at all the points on the Gaussian surface. The magnitude of →E is also the same at all points due to the spherical symmetry of the charge distributtion
Hence E∮Gaussion surfacedA=Qε0 .......(2)
But ∮Curved surfacedA total area of Gaussian surface surface =4πr2. Substituting this in equation (2), E.4πr2=Qε0
E.4πr2=Qε0(or)E=14πε0Qr2
In vector form →E=14πε0Qr2ˆr ......(3)
(iv) The electric field is radially outward if Q>0 and radially inward if Q<0. Form equation (3), the electric field at a point outside the shell will be same as if the entire charge Q is concentrated at the center of the spherical shell.
Case (b): At a point on the surface of the shperical shell (r=R): The electrical field at points on the spherical shell (r=R) is given by
→E=Q4πε0R2ˆr ......(4)
Case (c) At a point inside the spherical shell (r<R): Consider a point P inside the shell at a distance r from the center. A Guassian sphere of radius r is constructed as shown in the Figure (b). Applying Gauss law
∮Gaussion suface→E.d→A=Qε0
E.4πr2=Qε0 ......(5)
Since Gaussian surface encloses no charge, So Q=0. The equation (5) becomes
E=0 (r<R) .......(6)
The electric field due to the uniformly charged spherical shell is zero at all points inside the shell. A graph can be plotted between the electric field and radial distance. This is shown in Figure.
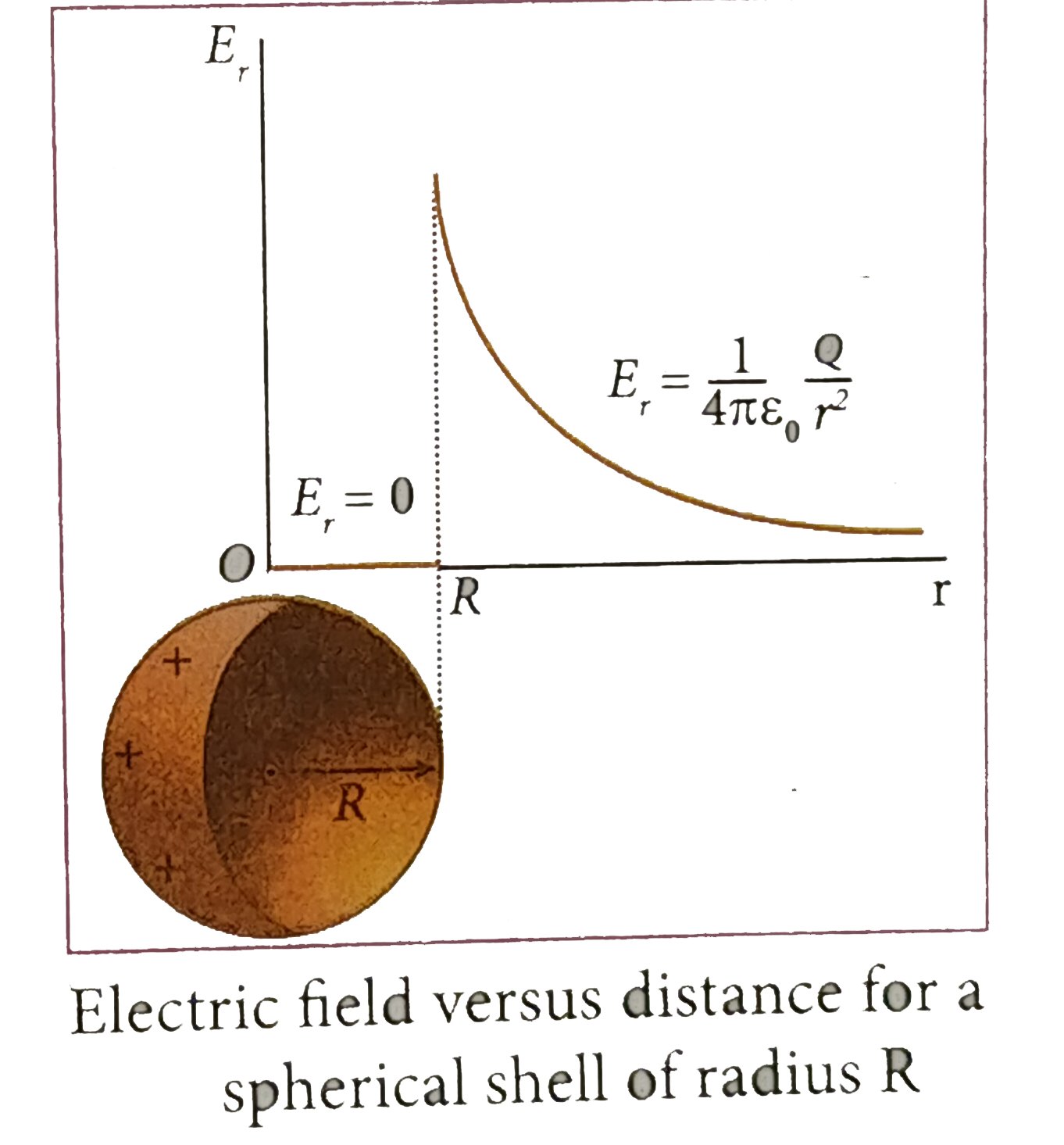
Similar Questions
Obtain an expression for electric field intensity due to uniformly charged spherical shell or hollow sphere.
View SolutionDerive an expression for electric field due to a uniformly charged spherical shell. i) at a point outside the shell
View SolutionDeduce the expression of field at P due to a uniformly charged thin spherical shell when the point,P is inside the shell.
View SolutionDerive the expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell
View SolutionDerive the expression for electric field intensity due to a uniformly charged thin spherical shell
at a point inside the shell.
View SolutionDraw the electric field lines due to a uniformly charged thin spherical shell when charge on the shell is positive?
View SolutionDraw the electric field lines due to a uniformly charged thin spherical shell when charge on the shell is
negative?
View SolutionState Gauss' law and using this law , derive an expression for the electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View Solution
