Assertion: If I is the incentre of △ABC,then|vec(BC)| vec(IA) +|vec(CA)| vec(IB) +|vec(AB)| vec(IC) =0Reason:IfOistheorig∈,thentheposition→−−→rofcentrof/_\ABCis−−→OA+−−→OB+−−→OC3 Solution in Kannada
Both A and R are correct and R is the correct explanation of A
Both A and R are correct but R is not the correct explanation of A
A is correct but R is incorrect
R is correct but A is incorrect
The correct Answer is:B
We know that,
OI=|CB|OA+|CA|OB+|AB|OC|BC|+|CA|+|AB|
and OG=OA+OB+OC3
Similar Questions
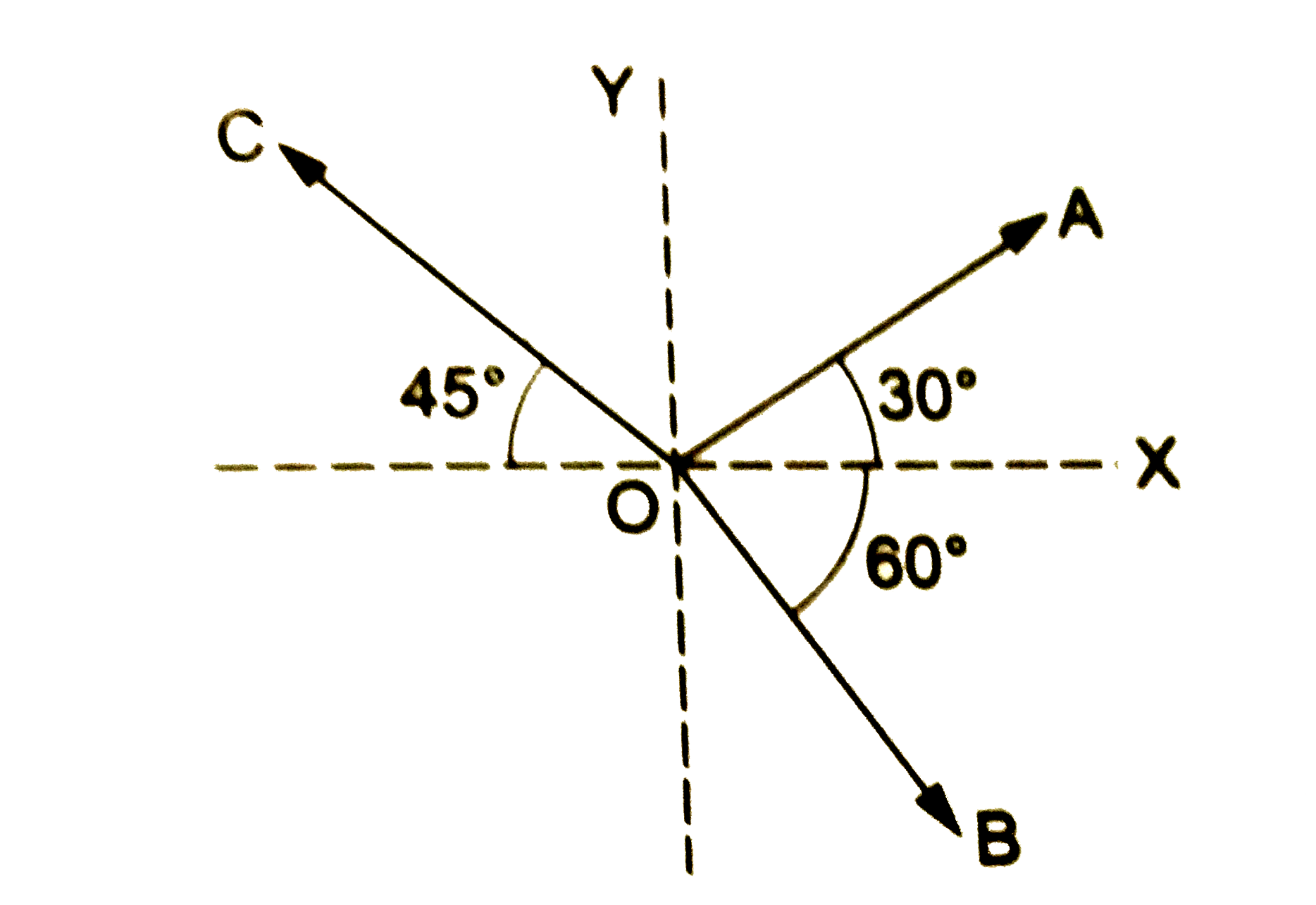
दिखाए गए वेक्टरो −−→OA,−−→OB तथा −−→OC के परिमाण बराबर है। वेक्टर −−→OA+−−→OB−−−→OC की दिशा बताएँ।
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionIf I is the centre of a circle inscribed in a triangle ABC, then ∣∣∣−−→BC∣∣∣−→IA+∣∣∣−−→CA∣∣∣−→IB+∣∣∣−−→AB∣∣∣−→IC is
View SolutionIf O is the circumcentre, G is the centroid and O' is orthocentre or triangle ABC then prove that: −−→OA+−−→OB+−−→OC=−−−→OO'
View Solution
