If $α, β$ be the roots of $4 x^{2} - 16 x + c = 0, c \in R$ such that $1 < α < 2 and 2 < β < 3$ , then the number of integral values of c is Solution in Kannada

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

$∵ 4 x^{2} - 16 x + c = 0$
$\Rightarrow x^{2} - 4 x + \frac{c}{4} = 0$
Let $f (x) = x^{2} - 4 x + \frac{c}{4}$
Then the following case arises:

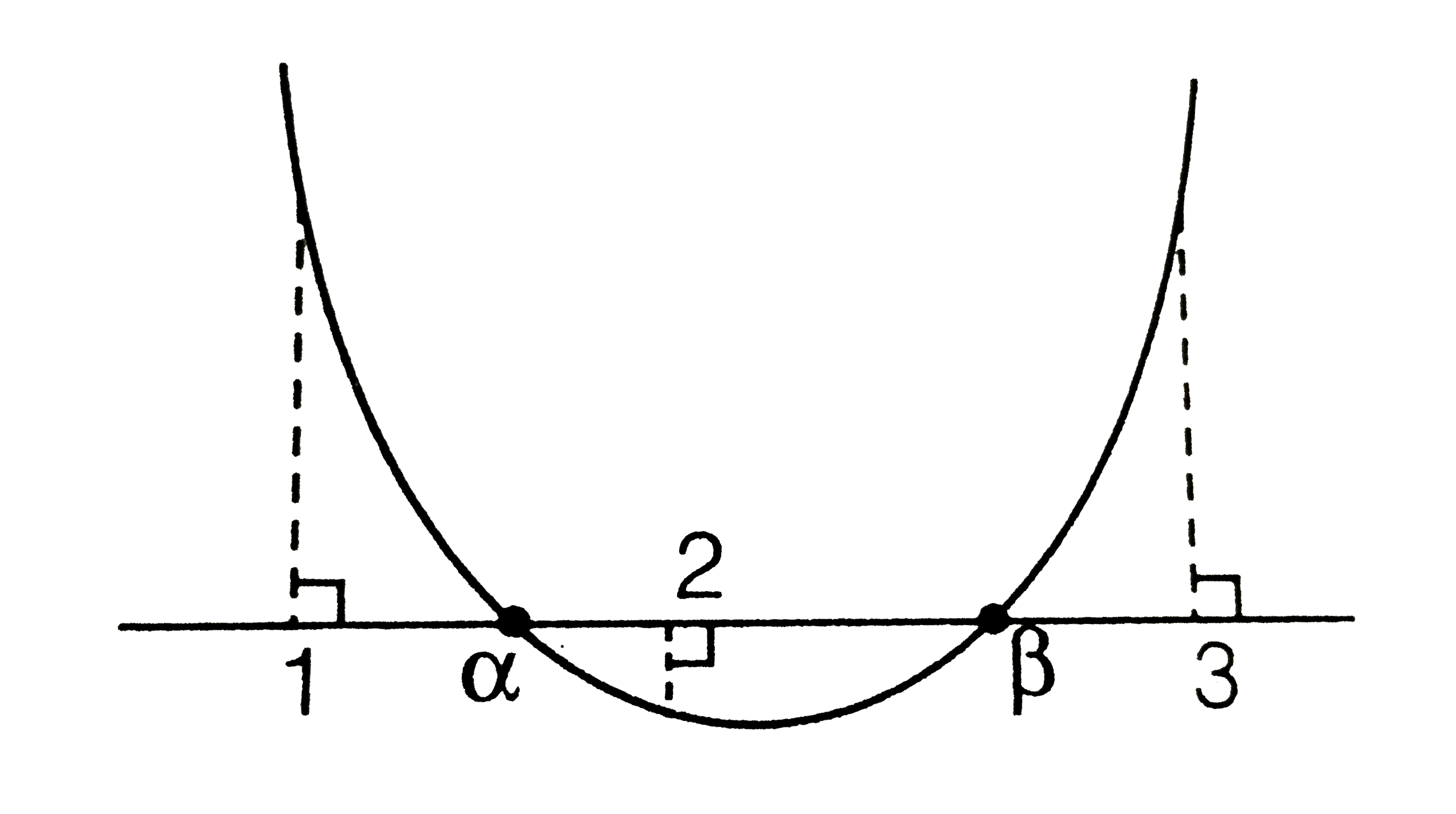
Case I $D > 0$
$= 16 - c > 0$
$∴ c < 16$
Case II $f (1) > 0$ ltbr $\Rightarrow 1 - 4 + \frac{c}{4} > 0$
$\Rightarrow \frac{c}{4} > 3$
$∴ c > 12$
Case III $f (2) < 0$
$\Rightarrow 4 - 8 + \frac{c}{4} < 0$
$\Rightarrow \frac{c}{4} < 4$
$c < 16$
Case IV $f (3) > 0$
$\Rightarrow 9 - 12 + \frac{c}{4} > 0$
$\Rightarrow \frac{c}{4} > 3$
$\Rightarrow c > 12$
Combining all cases, we get
$12 < c < 16$
Thus, integral values of c are 13, 14 and 15.
Hence number of integral values of c is 3.

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile