The value of a for which the equation (1−a2)x2+2ax−1=0 has roots belonging to (0,1) isSolution in Kannada
(a) a>0
(b) a<0
(c) a>2
(d) none of these
The correct Answer is:C
∵(1−a2)x2+2ax−1=0
1−a2≠0
x2−(2a1−a2)x−(11−a2)0
Let f(x)=x2+(2a1−a2)x−(1(1−a2))
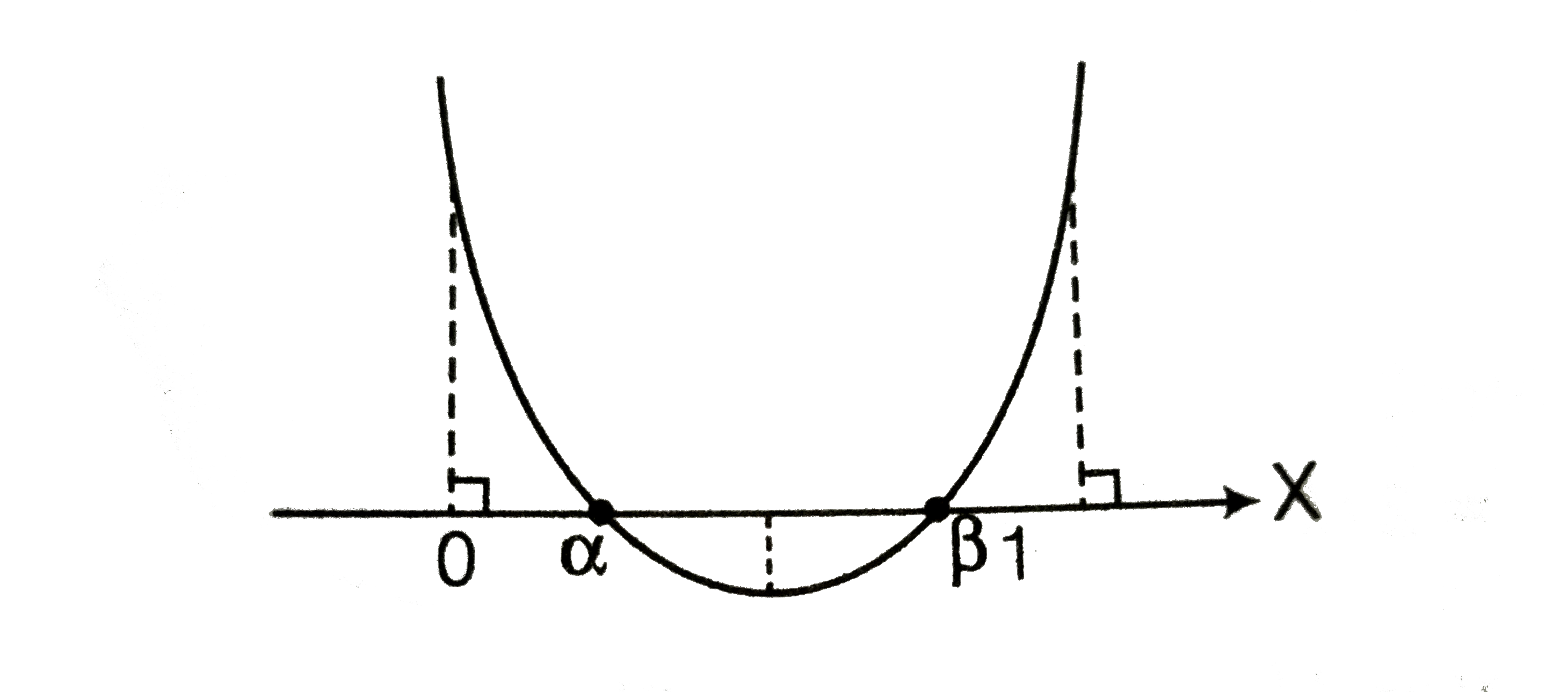
The following cases arise:
Case I D≥0 ltbr> (2a1−a2)2−4.1.(−11−a2)≥0
⇒4a2(1−a2)2+4(1−a2)≥0
⇒4a2+4−4a2(1−a2)2≥0
⇒4(1−a2)2≥0 [always true]
CaseII f(0)>0
⇒−1(1−a2)>0⇒11−a2<0
⇒1−a2<0
∴aε(−∞,o−1)∪(1,∞)
Case III f(1)>0
⇒1+2a(1−a2)−1(1−a2)>0
⇒1−a2+2a−1(1−a2)>0⇒a2−2a1−a2lg0

⇒a(a−2)(a+1)(a−1)>0
∴aε(−∞,−10∪(0,1)∪(2,∞)
Case Iv 0<x coordiane of vertex <1
⇒0<−2a2(1−a2)<1⇒0<aa2−1<1
⇒0<a(a+1)(a−1) an 1=aa2−1>0
⇒a(a+1)(a−1)>0

⇒aε(−1,0)∪(1,∞)
and (a−1+√52)(a−1−√52)(a+1)(a−1)>0
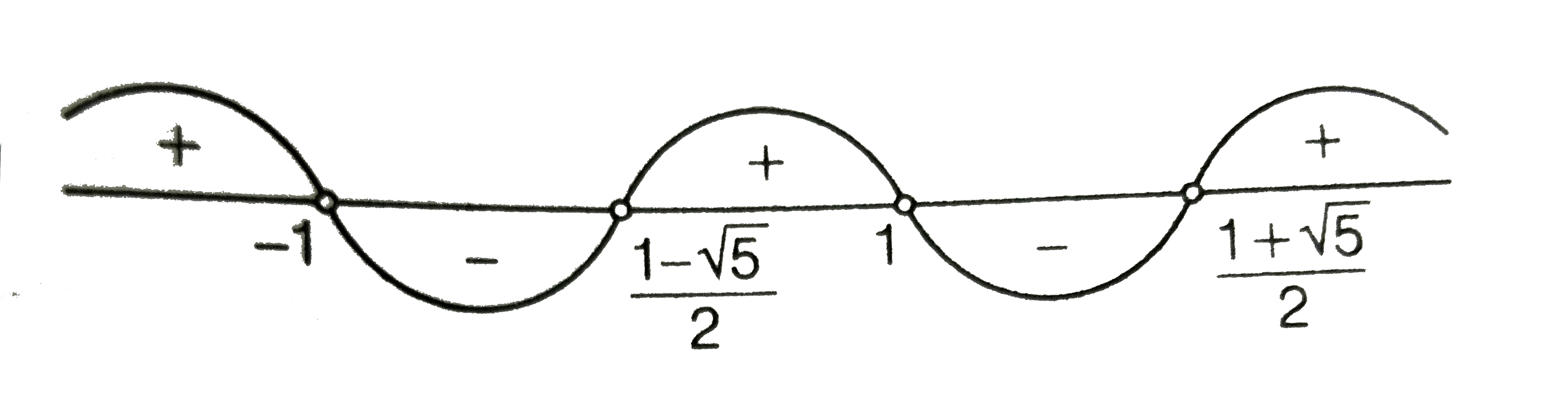
and aε(−∞,−1)∪(1−√52,1)∪(1+√52,∞)
∴aε(1−√52,0)∪(1+√52,∞)
Combining all cases, we get
Similar Questions
The value of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1, will always be greater than
View SolutionIf the equation x2−2ax+a2+a−3=0 has exactly one real root in (1,3) then largest integral value of a is
View SolutionThe equation x2+2(γ+1)x+a(a−4)=0 has negative roots only if γ belongs to the interval _________ .
View SolutionFor what values of the parameter a the equation x4+2ax3+x2+2ax+1=0 has atleast two distinct negative roots?
View SolutionThe necessary and sufficient condition for the equation (1−a2)x2+2ax−1=0 to have roots lying in the interval (0,1) is
View SolutionThe value of a for which the equationx3+2ax+2=0 and x4+2ax2+1=0 have a common root is "
View SolutionThe values of 'K' for which the equation |x|2(|x|2–2k+1)=1−k2, has No root, when k belongs to
View SolutionThe value of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1, will always be greater than
View Solution
