Solve the equation x3−[x]=3, where [x] denotes the greatest integer less than or equal to x.Solution in Kannada

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have x3−[x]=3
⇒x3−3=[x]
Let f(x)=x3−3 and g(x)=[x]
It is clear from the graphs, the point of intersection of two curves y=f(x) and y−g(x) lies between (1,0) and (2,0).
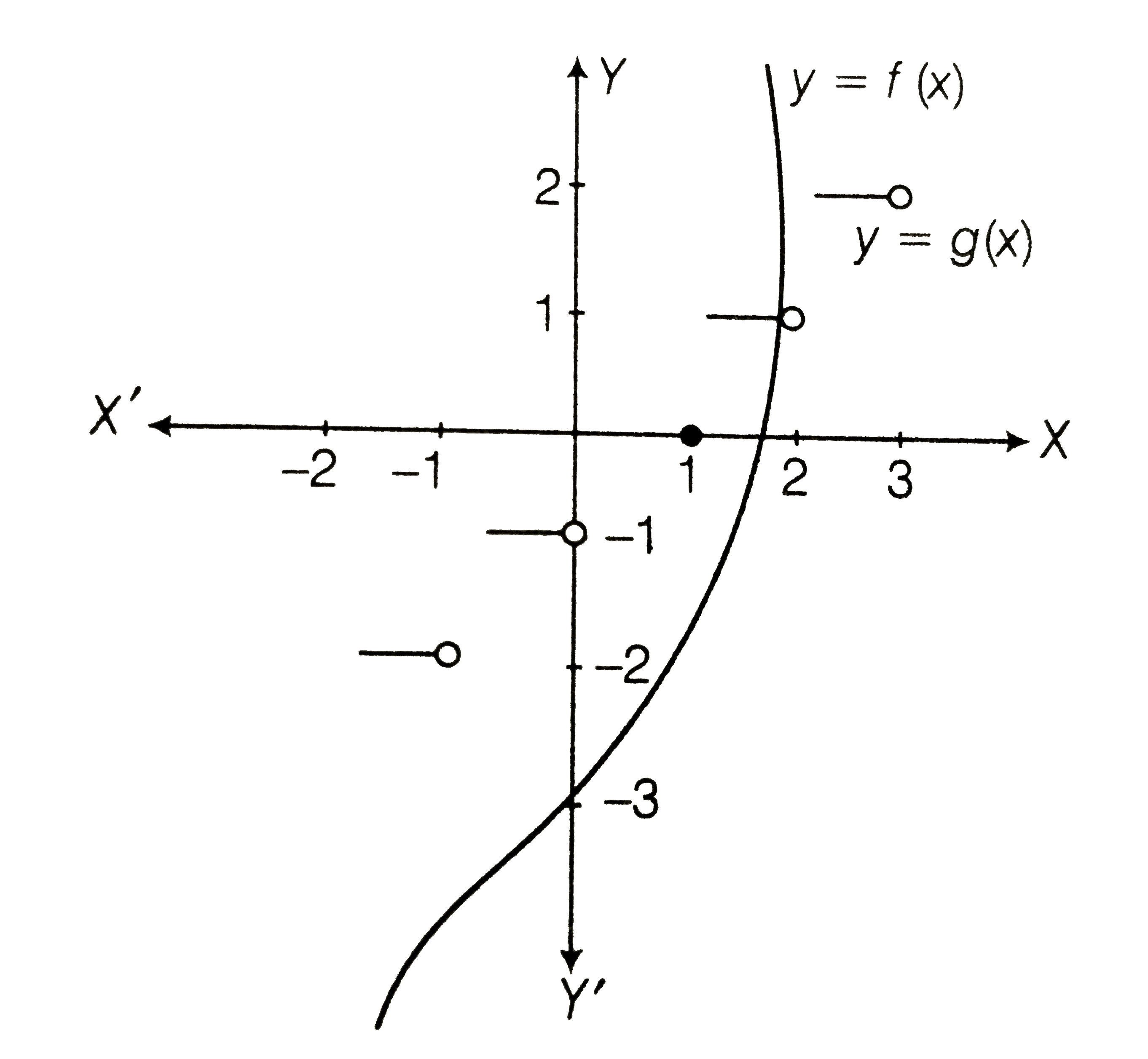
ocr_image
∴1<x<2
We have f(x)=x3−3 and g(x)=1
or x3−3=1⇒x3=4
∴x=(4)1/3
Hence x=41/3 is the solution of the equation x3−[x]=3
Aliter
∵x=[x]+f,0≤f<1
Then given equation reduces to
x3−(x−f)=3⇒x3−x=3−f
Hence it follows that
2<x3−x≤3
⇒2<x(x+1)(x−1)≤3
Further for x≥2, we have x(x+1)(x−1)≥6<3
For x<−1, we have x(x+1)(x−1)<0<2
For x=−1, we have x(x+1)(x−1)=0<2
For −1<x≤0, we have x(x+1)(x−1)≤−x<1
adn for 0<x≤1, we have x(x+1)(x−1)<x<x3≤1
Therefore x must be 1<x<2
∴[x]=1
Now the original equation can be written as
x3−1=3⇒x3=4
Hence x=41/3 is the solution of the given equation.

Updated on:21/07/2023
|