Solve the inequality (x+3)(3x−2)5(7−x)3(5x+8)2≥0.Solution in Kannada
Video Solution
Text Solution
We have (x+3)(3x−2)2(7−x)2(5x+8)2≥0
⇒−(x+3)(3x−2)5(x−7)3(5x+8)2≥0
⇒(x+3)(3x−2)5(x−7)3(5x+8)2≤0
[take before x,+ve sign in all brackets]
The critial points are (−3),(−85),23,7.
Hence xε(−∞,−3)∪[23,7]∪{−85}.
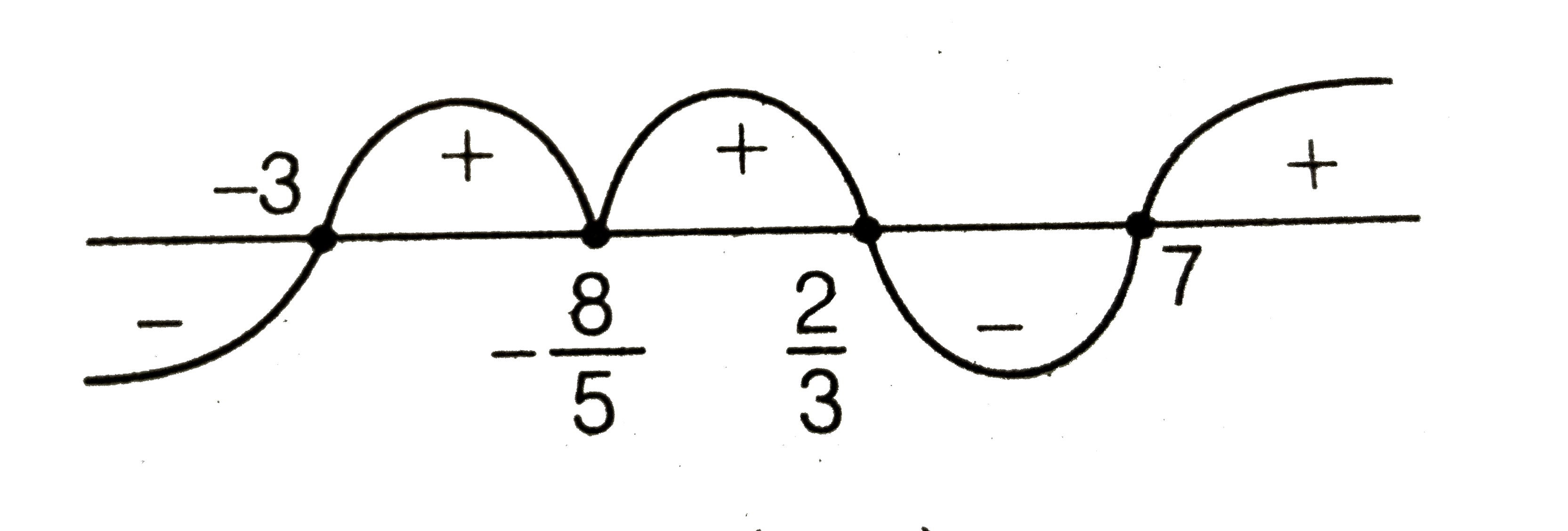
|
Updated on:21/07/2023
Similar Questions
Solve: 5x3x−3+6x+2=53
03:42View SolutionSolve the following linear inequation in R:x5<3x−24−5x−35
03:26View SolutionSolve the inequality x2≥5x−23−7x−35
02:59View Solutionx के लिए हल कीजिए-
8(5x+1)+7(2x+3)=13(3x+5)+2(2x+4)03:03View SolutionLimx→0x3√x2+3x+8−3√x2−5x+8=
View SolutionSolve: 4^((2x+3)/2) * 8^((x+3)/3)=2^((5x+7)/3) * 16^((3x-1)/3)
07:56View SolutionSolve the inequation: 3(x−2)≤5x+8
01:25View SolutionSolve the inequalities given below for real x :- 37−(3x+5)≥9x−8(x−3)
05:47View Solution
