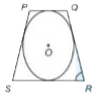
A circle touches all the sides of a quadrilateral PQRS, whose sides. PQ=2cm, QR =3cm and RS= 4cm. What is the length of PS?
3 cm
2 cm
1 cm
4 cm
The correct Answer is:A
To find the length of side PS in the quadrilateral PQRS, we can use the property of tangential quadrilaterals. In such quadrilaterals, the sum of the lengths of opposite sides is equal.
1. Identify the sides of the quadrilateral:
- Given:
- PQ = 2 cm
- QR = 3 cm
- RS = 4 cm
- PS = ? (This is what we need to find)
2. Apply the property of tangential quadrilaterals:
- The property states that for a quadrilateral with an inscribed circle (tangential quadrilateral), the sum of the lengths of opposite sides is equal:
PQ+RS=QR+PS
3. Substitute the known values into the equation:
- Substitute PQ, QR, and RS into the equation:
2+4=3+PS
4. Simplify the equation:
- Calculate the left side:
6=3+PS
5. Isolate PS:
- To find PS, subtract 3 from both sides:
PS=6−3
PS=3 cm
Final Answer:
The length of PS is 3 cm.
- Given:
- PQ = 2 cm
- QR = 3 cm
- RS = 4 cm
- PS = ? (This is what we need to find)
- The property states that for a quadrilateral with an inscribed circle (tangential quadrilateral), the sum of the lengths of opposite sides is equal:
PQ+RS=QR+PS
- Substitute PQ, QR, and RS into the equation:
2+4=3+PS
- Calculate the left side:
6=3+PS
- To find PS, subtract 3 from both sides:
PS=6−3
PS=3 cm
The length of PS is 3 cm.
Similar Questions
Knowledge Check
In the figure, a circle touches all the four sides of a quadrilateral ABCD whose sides AB= 6.5 cm, BD= 5.4 cm and CD = 5.3 cm . The length of AC is :
 A4.6 cmB5.8 cmC6.2 cmD6.4 cm
A4.6 cmB5.8 cmC6.2 cmD6.4 cmIf the sides of a quadrilateral ABCD touch a circle and AB = 6 cm, CD = 5 cm BC = 7 cm, then the length of AD (in cm) is
A4B6C8D9If the sides of a quadrilateral ABCD touch a circle and AB = 6 cm, CD = 5 cm, BC = 7 cm, then the length of AD in cm is :
Aa) 8Bb) 9Cc) 4Dd) 6
A circle touches all the four sides of a quadrilateral ABCD. If AB = 9 cm, BC= 8 cm and CD = 12 cm, then what is DA equal to?
View SolutionConstruct a parallelogram PQRS, when PQ =3.7cm, QR =2.3 cm and PR=4.8 cm.
View SolutionIn ΔPQR ∠R=∠P and QR=4cm and PR=5cm Then the length of PQ is
View SolutionPQRS is a cyclic quadrilateral in which PQ = 14.4 cm, QR = 12.8 cm and SR = 9.6 cm. If PR bisects QS, what is the length of PS? PQRS एक चक्रीय चतुर्भुज है जिसमें PQ = 14.4 cm, QR = 12.8 cm और SR = 9.6 cm है। यदि PR, QS को समद्विभाजित करता है, तो PS की लंबाई क्या है?
View SolutionIn the given figure, a circle touches the sides of the quadrilateral PQRS. The radius of the circle is 9cm. ∠RSP=∠SRQ=60∘and∠PQR=∠QPS=120∘. What is the perimeter (in cm) of the quadrilateral?
View Solution
