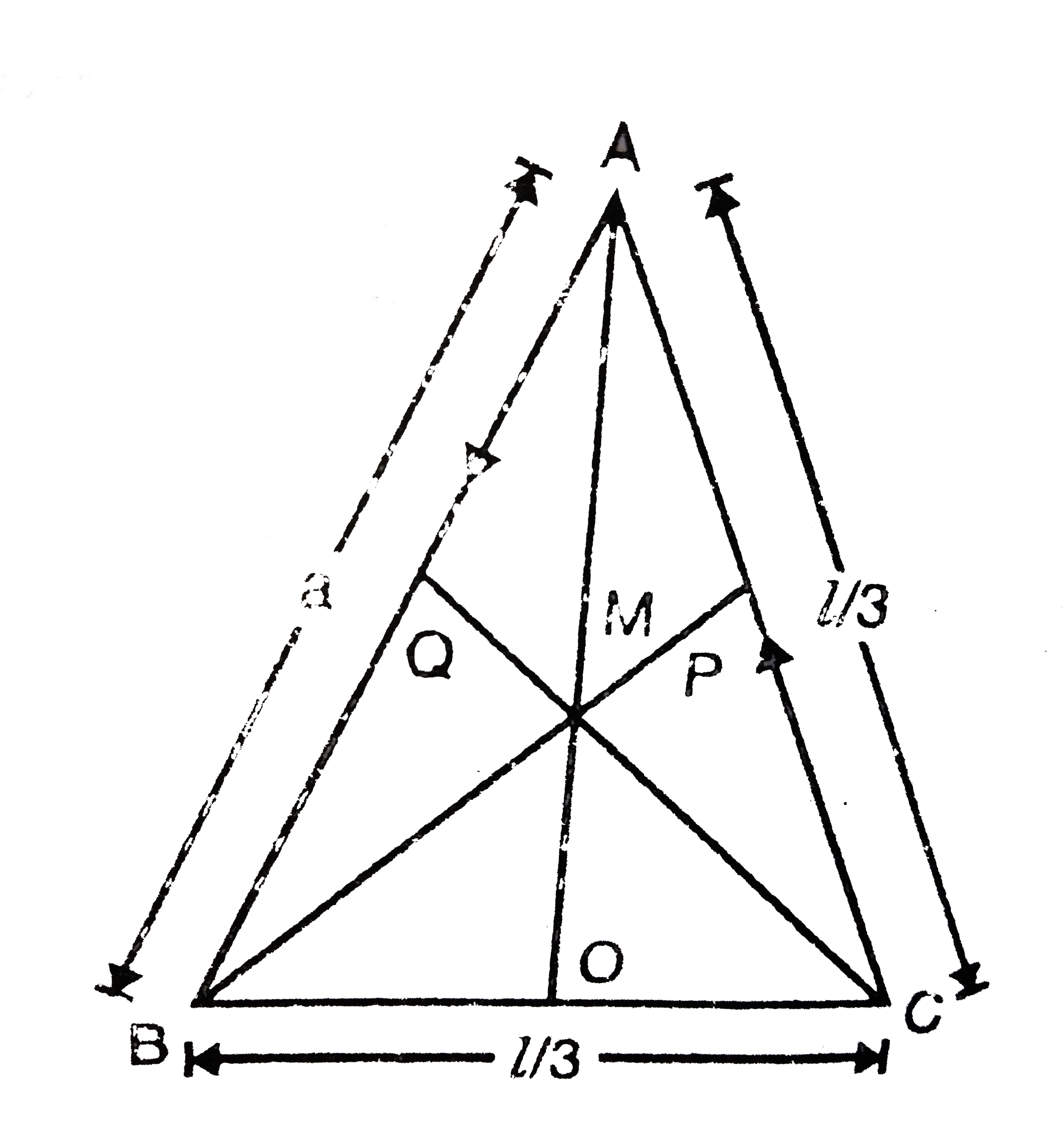
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?Solution in Tamil

Video Solution

Text Solution

Verified by Experts

$A_{0} = \sqrt{{(\frac{1}{3})}^{2} - {(\frac{1}{6})}^{2}}$
$= l S q r t (\frac{1}{9} - \frac{1}{36} = l . \sqrt{\frac{4 - 1}{36} = l \sqrt{\frac{1}{12}}}$
$∴ M O, M P, M Q = \frac{l}{3} \times \frac{1}{2} \frac{\sqrt{1}}{3} = \frac{1}{6 \sqrt{3}}$
So, B at $M = 3 \frac{μ_{o} i}{4 π} . \frac{36 \times 3}{12} . \frac{l}{3} 2 [\frac{1}{2}]$
$= \frac{27 μ_{o} i}{π l} a l o n g \otimes$
(b) Solve as above.

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

HC VERMA-MAGNETIC FIELD DUE TO CURRENT-exercise

Home
Ask Doubt
Profile