Locate the image of the point object O in the situtaion shown. The point C denotes the centre of curvature of the separating surface. Solution in Tamil
Here u=-15cm, R=30cm, μ1=1andμ2=1.5. We have <br>mu_2/v-mu_1/u=(mu_2-mu_1)/R<br>or, 1.5/v-1.0/(-15cm=(1.5-1)/(30cm)<br>or (1.5c=0.530cm−115cm)
v=−30
The image is formed 30 cm left to the spherical surface and is virtual.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Worked out Examples
28 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
19 Videos
- GAUSS LAWBOOK - HC VERMACHAPTER - GAUSS LAWEXERCISE - Exercises
24 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
Similar Questions
An object is placed on the principal axis of concave mirror of focal length 10 cm at a distance of 8.0 cm from the pole. Find the position and the nature of the image.
View SolutionIs the formula "Real depth/Apparent depth =μ. valid if viewed from a position quite away from the normal ?
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
View SolutionA spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O, and PO=OQ. The distance PO
View SolutionIn the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is

View SolutionA spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The center of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The ling PQ cuts the surface at a point O, and PO=OQ. The distance PO is equal to
View SolutionLocate the image of the point object O . The point C is centre of curvature of the spherical surface.
View SolutionTwo cancave refracting surfacwe of equal radii fo curvature face each other in air as shown in figure. A point object O is placed midway between the centre and one of the poles. Then the separation between the images of O formed by each refracting surface is
View Solutionचित्र में दिखाई गई परिस्थिति में वस्तु O के प्रतिबिंब का स्थान निर्धारित करें । बिंदु C दोनों माध्यमों की उभयनिष्ठ (COMMON) गोलीय सतह का वक्रता - केंद्र हैं ।
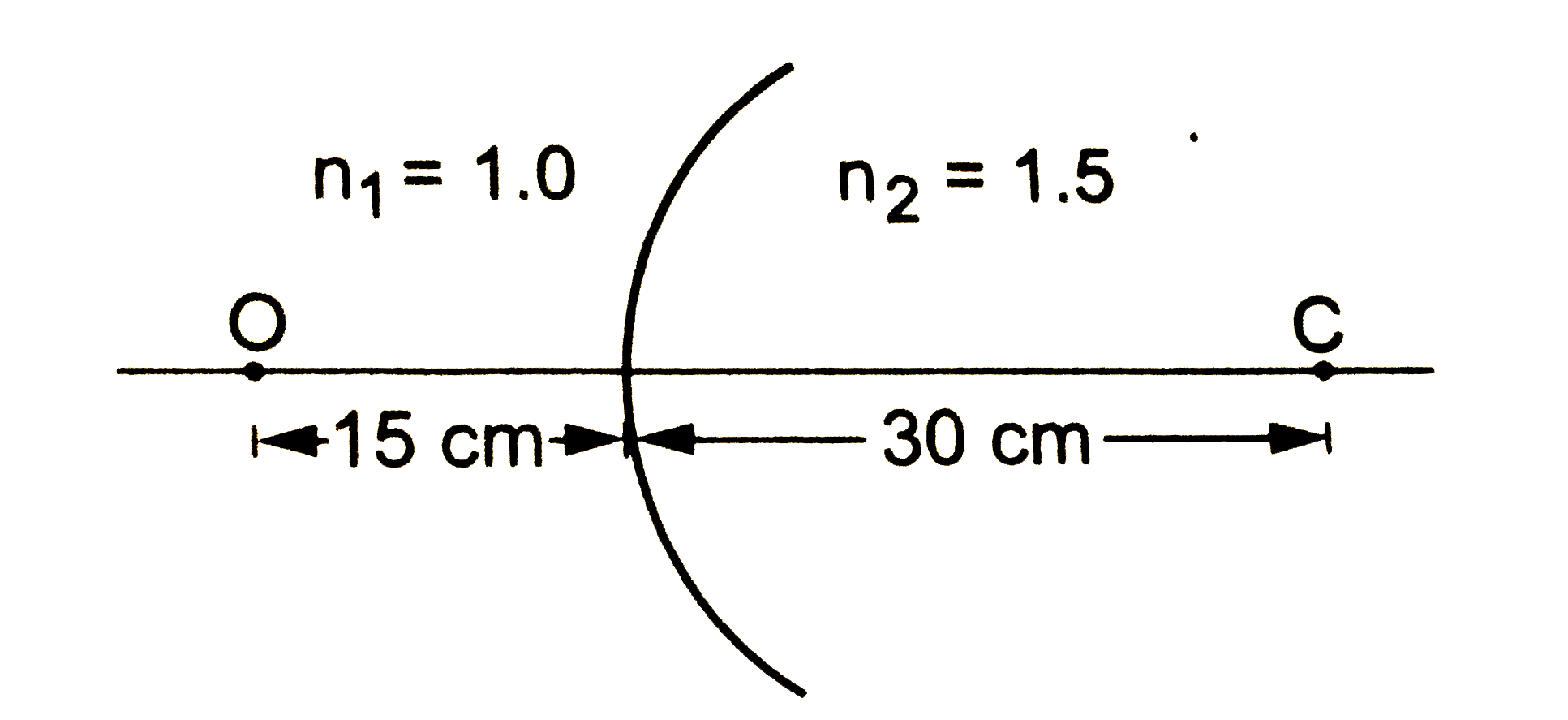
View SolutionLocate the image of the point object O in the situtaion shown. The point C denotes the centre of curvature of the separating surface.
View SolutionA spherical surface of radius of curvature R, separates air (refractive index 1.0) fromglas (refractive index 1.5). The centre of curvature is in the glass. A point object P in air is found to have a real image Q in the glass.The line PQ cuts the surface at a point O and PO =OQ. The distance PO is equal to
View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View SolutionLocate the image of the point object O in the situation shown in figure. The point C denotes the centre of curvature of the separating surface.

View SolutionLocate the image formed by refraction in the situation shown in figure. The point C is the centre of curvature

View SolutionA spherical surface of radius of curvature R, separates air (refractive index 1.0) from glass (refractive index 1.5) The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O and PO=OQ. The distance PO is equal to
View Solution
