The block shown in figure has a mass M and descends with an acceleration a. The mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.
 Solution in Tamil
Solution in Tamil
Consider the block + the part of the string below A as the system . Let the tension at A be T. The forces acting on this system are
a. (M+mg) g, downward, by the earth
T, upward, by the upper part of the string.
The first is gravitational and the second is electromagnetic. We do not have to write the force by the string on the block. This electromagnetic force is by one part of the system on the other part. Only the forces acting on the system by the objects other than the system are to be included.
The system is descending with an acceleration a. Taking the downward direction as the Y-axis, the total force along the X-axis is (M+m)g−T. Using Newton's law along the X-axis is (M+m)g−T=(M+m)a.
or T=(M+m)(g−a)...........(i)
we have omitted the free body diagram. This you can do if you can draw the free body diagram in your mind and write the equations correctly.
To get the tension T' at the lower end we can put m=0 in i.
Effectively we take the point A at the lower end. Thus, we get T'=M(g−a).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples
11 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
A body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionIf the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
View SolutionShould the internal energy of a system necessarily increase if heat is added to it?
View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionThe mass of the part of the string below A i figure is m. Find the tension of he string at the lowere end and at A.
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).
View SolutionFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms^(-2)
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g//3 . The work done by the string is
View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m//s^(2))
View SolutionA bock of mass M is on a horizontal table and is connected to an inextensible string. The string passes over a frictionless pulley fitted at one edge of the table. At the other end, another block of mass m hangs vertically. Coefficient fo friction between the table and the block of mass is mu . Find the acceleration of the system. Also find the tension in the string.
View SolutionThe mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View Solutionजैसा कि आकृति में दिखाया गया है कि एक डोरी द्रव्यमान M और त्रिज्या R की घिरनी (चकती) पर लिपटी हुई है। डोरी के एक सिरे पर, द्रव्यमान M का एक गुटका जुड़ा है और दूसरे सिरे में (a) 2 Mg का बल और (b) द्रव्यमान 2 M का एक गुटका जुड़ा है। Aऔर B में क्रमश: αA और αB चकती के कोणीय त्वरण हैं, तब: (घिरनी पर डोरी फिसल नहीं रही है)
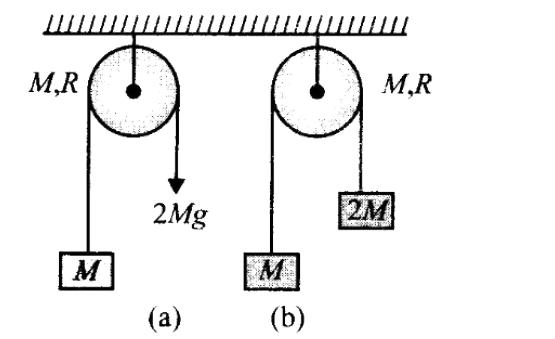
View Solution
