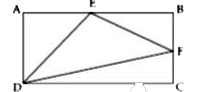
ABDC is a parallelogram in which diagonals AD and BC intersect at O. AE and DF are perpendiculars on BC at E and F, respectively . Which of the following is NOT true?
A) ΔADC=~ΔABD
B) ΔAOE=~ΔDOF
C) ΔABC=~ΔDCB
D) ΔAEB=~ΔDFC
The correct Answer is:A
To solve the problem, we need to analyze the properties of the parallelogram ABCD and the triangles formed by its diagonals and the perpendiculars AE and DF.
1. Identify the Parallelogram and Diagonals:
- We have a parallelogram ABCD with diagonals AC and BD intersecting at point O.
2. Understanding the Perpendiculars:
- AE is a perpendicular dropped from point A to line BC at point E.
- DF is a perpendicular dropped from point D to line BC at point F.
3. Triangles Formed:
- We can identify two triangles of interest: triangle ABE and triangle DCF.
- Since AE and DF are perpendicular to BC, both triangles ABE and DCF are right triangles.
4. Properties of Parallelograms:
- In a parallelogram, opposite sides are equal, and opposite angles are equal.
- The diagonals bisect each other, meaning AO = OC and BO = OD.
5. Similar Triangles:
- Since AE and DF are both perpendicular to BC, triangles ABE and DCF can be compared.
- We can conclude that triangles ABE and DCF are similar due to the AA (Angle-Angle) criterion for similarity (both have a right angle and share angle ADB).
6. Analyzing Options:
- We need to check which statement about the triangles or the parallelogram is NOT true.
- We can compare the angles and sides of triangles ABE and DCF to see if any statements contradict the properties of the parallelogram or the similarity of triangles.
7. Conclusion:
- After analyzing the properties and relationships, we determine which statement is incorrect based on the properties of the parallelogram and the similarity of the triangles.
- We have a parallelogram ABCD with diagonals AC and BD intersecting at point O.
- AE is a perpendicular dropped from point A to line BC at point E.
- DF is a perpendicular dropped from point D to line BC at point F.
- We can identify two triangles of interest: triangle ABE and triangle DCF.
- Since AE and DF are perpendicular to BC, both triangles ABE and DCF are right triangles.
- In a parallelogram, opposite sides are equal, and opposite angles are equal.
- The diagonals bisect each other, meaning AO = OC and BO = OD.
- Since AE and DF are both perpendicular to BC, triangles ABE and DCF can be compared.
- We can conclude that triangles ABE and DCF are similar due to the AA (Angle-Angle) criterion for similarity (both have a right angle and share angle ADB).
- We need to check which statement about the triangles or the parallelogram is NOT true.
- We can compare the angles and sides of triangles ABE and DCF to see if any statements contradict the properties of the parallelogram or the similarity of triangles.
- After analyzing the properties and relationships, we determine which statement is incorrect based on the properties of the parallelogram and the similarity of the triangles.
Similar Questions
Knowledge Check
ABCD is a parallelogram. The diagonals AC and BD intersect at a point O. If E,F,GandH are the mid-points of AO,DO,COandBO respectively, then the ratio of (EF+FG+GH+HE) to (AD+DC+CB+BA) is:
A1:1B1:2C1:3D1:4ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A0.042361111111111B0.043055555555556C0.04375D0.044444444444444From a point O in the interior of a ΔABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2
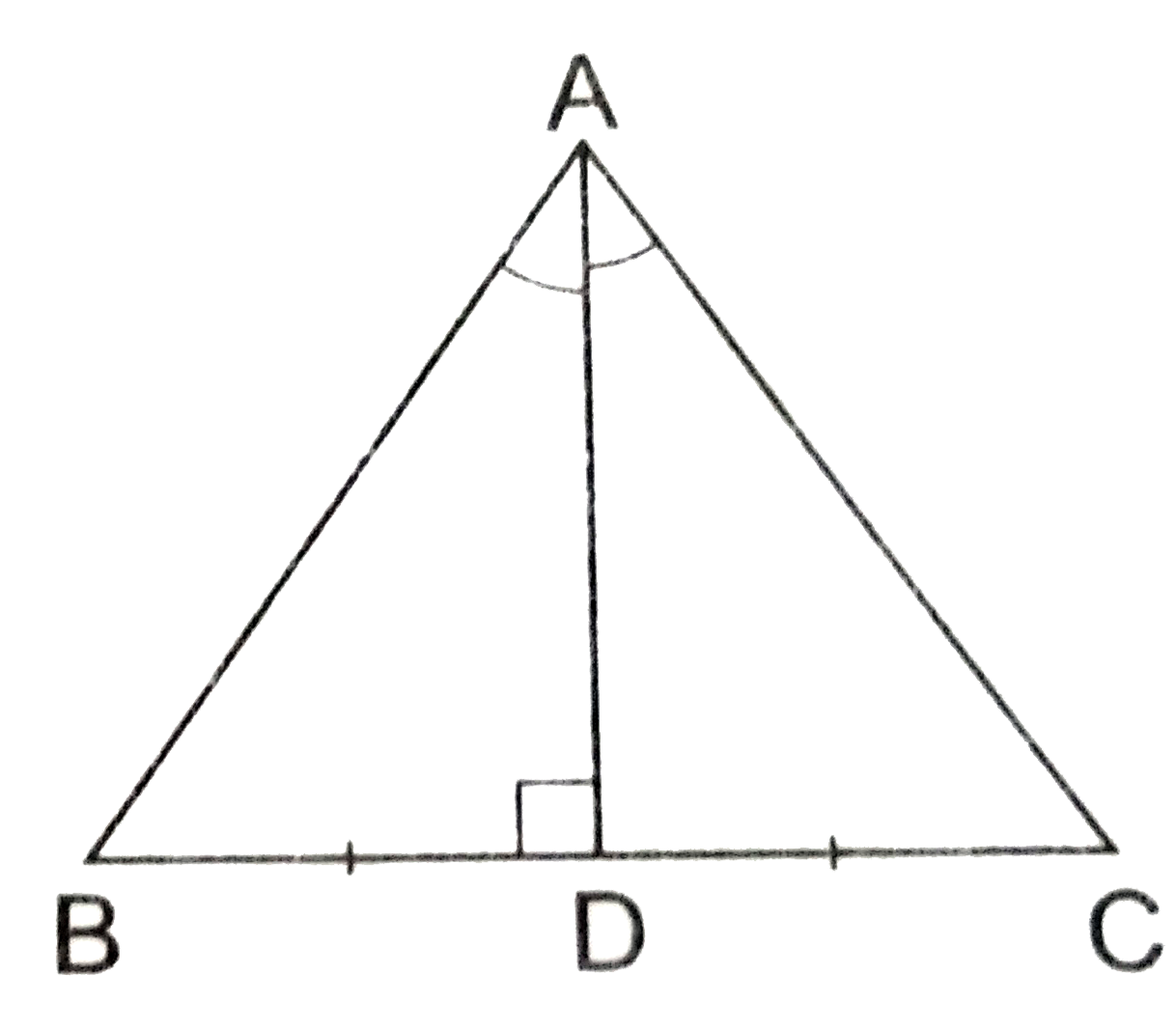
In an equilateral triangle ABC, if AD⊥BC then which of the following is true?
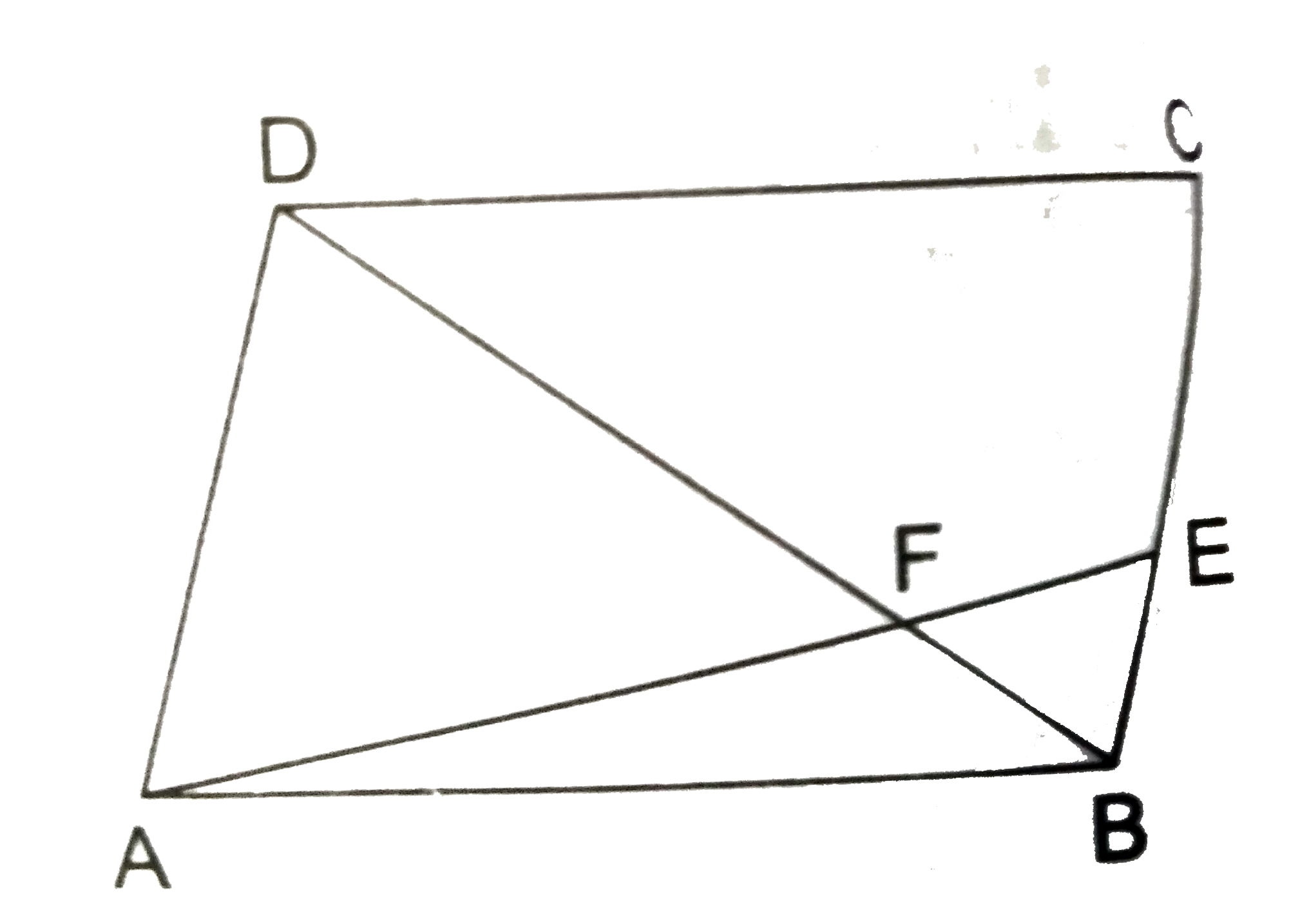
View SolutionABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
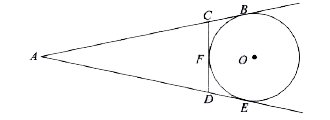
View SolutionIn the figure , if AD, AE and BC are tangent to the circle at D,E and F , respectively , then
View SolutionIn ΔABC,∠A=90∘. From point A, perpendicular AD is drawn to side BC. Which one of the following is true ?
View SolutionFrom a point O in the interior of a DeltaABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
View Solution