समीकरण F=14πε0.q1q2r2, जहां प्रतीकों का सामान्य अर्थ है, में निर्वात के परावैद्युतांक (ε0) के लिए विमीय सूत्र, है
[M1L3A−2T−4]
[M−1L−3T4A2]
[M−1L−3A−2T−4]
[M1L3T2A−4]
The correct Answer is:B
जैसा कि, F=14πε0q1.q2r2
⇒ε0=q1.q24πFr2
=[TA]2[L2][MLT−2]
=[M−1L−3T4A2]
Topper's Solved these Questions
Similar Questions
12.5 वर्ष के अर्ध आयु के साथ ट्राइटियम β - क्षय से गुजरता है। 25 वर्ष बाद शुद्ध ट्राइटियम के एक नमूने का कितना अंश अविघटित रहेगा?
View Solutionv चाल से गतिमान एक H- परमाणु विराम अवस्था में एक अन्य H - परमाणु के साथ सम्मुख प्रत्यक्ष संघट्ट करता है। दोनों परमाणु मूल अवस्था में हैं। वेग v का न्यूनतम मान जिसके लिए कम से कम एक परमाणु उत्तेजित हो सकता है, है
View SolutionThe concentric, thin metallic spheres of radii r_(1) and r_(2) (r_(1) gt r_(2)) carry charges q_(1) and q_(2) respectively. Then the electric potential at distance r (r_(2) lt r lt r_(1)) will be (1)/(4pi epsilon_(0)) times
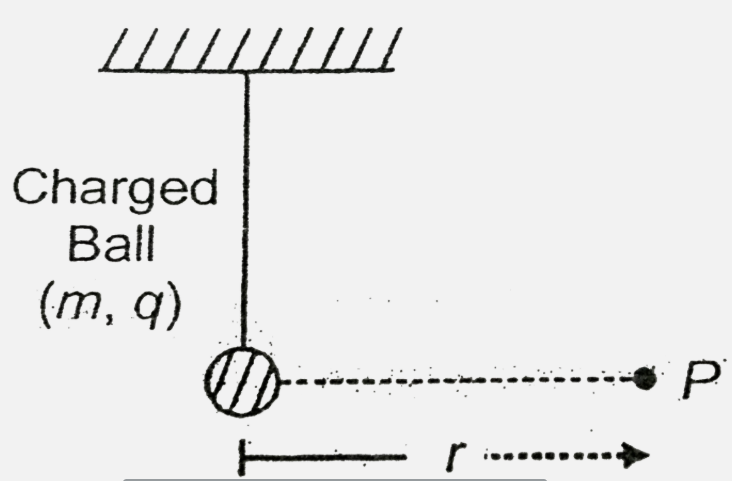
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
View SolutionTwo concentric thin metallic spherical shells of radii R_(1) and R_(2) (where R_(1) lt R_(2) ) are charged with q_(1) and q_(2) coulombs, respectively. Using Gauss' theorem show that, (i) the electric field intensity for radius r lt R_(1) is zero, (ii) the electic field intensity for radius r, where R_(1) lt r lt R_(2), is (1)/(4pi epsilon_(0)).(q_(1))/(r^(2)) and (iii) the electri field intensity for radius r gt R_(2) is (1)/(4pi epsilon_(0)).(q_(1)+q_(2))/(r^(2)) .
View SolutionThere are three charges Q1 columb Q2 columb and Q3 columb. Q2 and Q3 are fixed at positive (0,0) and (30,0) respectively.Now Q1 moves in circular path in x−y plane of radius 40m with help of external agent starting from (0,40) about origin then work done by external agent is till Q1 crosses x axis (40,0) given co-ordinates are in centimeters: (1) Q1Q34πε0 joule (2) Q1Q32πε0 joule (3) 2Q1Q3πε0joule (4) 2Q1(Q2+Q3)πε0 joule
View SolutionThere are three charges Q1 columb Q2 columb and Q3 columb. Q2 and Q3 are fixed at positive (0 0) and (30 0) respectively.Now Q1 moves in circular path in x -y plane of radius 40 cm with help of external agent starting from (0 40) about origin then work done by external agent is till Q1 crosses x axis (40 0) given co-ordinates are in centimeters: 1) Q1Q34πε0 joule 2) Q1Q32πε0 joule 3) 2Q1Q3πε0 joule 4) 2Q1(Q2+Q3)πε0 joule
View Solutionयदि दो आवेशों q1 व q2 जो एक - दूसरे से दूरी r पर स्थित है के बीच लगने वाला बल F निम्नलिखित सूत्र द्वारा दिया जाता है :
F=14πε0×q1q2r2
तो ε0 का विमीय सूत्र ज्ञात कीजिए।
View Solution[" Two uniformly charged non "],[" conducting spheres of radii "R_(1)" and "],[R_(2)" having charges "Q_(1)" and "Q_(2)],[" respectively are seperated by "],[" distance "r" .Total electrostatic "],[" energy of this system is "],[qquad [U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))+(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))-(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))-(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(R_(2))+(Q_(1)Q_(2))/(r)}]]
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
View Solutionλ का वह मान जिसके लिए द्विघात समीकरण x2+(3−λ)x+2=λ के मूलों के वर्गों के योग का मान न्यूनतम है , है ?
View Solutionयदि x में द्विघात समीकरण 3m2x2+m(m−4)x+2=0 के मुलो का अनुपात λ है तो m का वह न्यूनतम मान जिसके लिए λ+1λ=1 है, है
View SolutionAnswer carefully:
(a) Two large conducting spheres carrying charges Q1 and Q2 are brought close to each other. Is the magnitude of electrostatic force between them exactly given by Q1,Q2/4πε0r2, where r is the distance between their centres?
(b) If Coulomb’s law involved 1/r3 dependence (instead of would Gauss’s law be still true ?
(c) A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
(d) What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
(e) We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
(f) What meaning would you give to the capacitance of a single conductor?
(g) Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .

View Solution'ये एहतियात जरूरी है इस बहर के लिए पंक्ति में 'बहर' का' अर्थ क्या है?
View Solution
