In the group of 85 people speak three language English, French and Japanese. 15 people speak only the French language, 10 people speak only the English language. 10 people speak both French and English language, 20 people speak both Japanese and French language and 15 people speak both English and Japanese language. 10 people speak all three kinds of language. Find how many people speak only Japanese language?
(a)15
(b)10
(c)5
(d)12
15
10
5
12
The correct Answer is:C
To find the number of people who speak only Japanese, we can use the principle of inclusion-exclusion and the information given in the problem. Let's break down the steps:
Step 1: Define the Variables
Let:
- E: Number of people who speak English
- F: Number of people who speak French
- J: Number of people who speak Japanese
Step 2: Gather the Given Information
From the problem, we have:
- |F only|=15 (only French)
- |E only|=10 (only English)
- |E∩F|=10 (both English and French)
- |F∩J|=20 (both French and Japanese)
- |E∩J|=15 (both English and Japanese)
- |E∩F∩J|=10 (all three languages)
Step 3: Calculate the Total Number of People
The total number of people is given as 85.
Step 4: Calculate the Number of People Speaking Each Language
Using the information provided, we can calculate the total number of people who speak at least one language:
1. Only French: |F only|=15
2. Only English: |E only|=10
3. French and English but not Japanese: |E∩F|−|E∩F∩J|=10−10=0
4. French and Japanese but not English: |F∩J|−|E∩F∩J|=20−10=10
5. English and Japanese but not French: |E∩J|−|E∩F∩J|=15−10=5
6. All three languages: |E∩F∩J|=10
Step 5: Calculate the Total Count from the Above
Now, let's sum these values to find the total number of people who speak at least one language:
Total=|F only|+|E only|+|E∩F|+|F∩J|+|E∩J|+|E∩F∩J|
=15+10+0+10+5+10=50
Step 6: Find the Number of People Speaking Only Japanese
Now, we need to find the number of people who speak only Japanese. We know the total number of people is 85, so:
People speaking only Japanese=85−Total
=85−50=35
Step 7: Calculate the Number of People Speaking Only Japanese
Now we need to account for those who speak Japanese but not only Japanese. We have:
- People who speak both Japanese and French (including those who speak all three): 20
- People who speak both Japanese and English (including those who speak all three): 15
- People who speak all three languages: 10
Thus, the number of people who speak Japanese but not only Japanese is:
Japanese speakers=|F∩J|+|E∩J|−|E∩F∩J|=20+15−10=25
Step 8: Calculate Only Japanese Speakers
Finally, we can find the number of people who speak only Japanese:
Only Japanese=Total Japanese speakers−Japanese speakers not only=35−25=10
Conclusion
The number of people who speak only Japanese is 10.
Let:
- E: Number of people who speak English
- F: Number of people who speak French
- J: Number of people who speak Japanese
From the problem, we have:
- |F only|=15 (only French)
- |E only|=10 (only English)
- |E∩F|=10 (both English and French)
- |F∩J|=20 (both French and Japanese)
- |E∩J|=15 (both English and Japanese)
- |E∩F∩J|=10 (all three languages)
The total number of people is given as 85.
Using the information provided, we can calculate the total number of people who speak at least one language:
2. Only English: |E only|=10
3. French and English but not Japanese: |E∩F|−|E∩F∩J|=10−10=0
4. French and Japanese but not English: |F∩J|−|E∩F∩J|=20−10=10
5. English and Japanese but not French: |E∩J|−|E∩F∩J|=15−10=5
6. All three languages: |E∩F∩J|=10
Now, let's sum these values to find the total number of people who speak at least one language:
=15+10+0+10+5+10=50
Now, we need to find the number of people who speak only Japanese. We know the total number of people is 85, so:
=85−50=35
Now we need to account for those who speak Japanese but not only Japanese. We have:
- People who speak both Japanese and English (including those who speak all three): 15
- People who speak all three languages: 10
Finally, we can find the number of people who speak only Japanese:
The number of people who speak only Japanese is 10.
Similar Questions
(i) In a group of 50 people , 35 speak Hindi , 25 speak both English and Hindi and all people speak atleast one of the two languages . How may people speak only English and not Hindi ? How many people speak English?
(ii) In a group of people , 50 speak both English and Hindi and 30 people speak English but not Hindi All the people speak at least one of the two languages . How many people speak English ?View SolutionIn a group of 1000 people 700 can speak English and 500 can speak Hindi. If all the people speak atleast one of the two languages find : how many can speak exactly one language?
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, how many people speak only Italian and French language ?
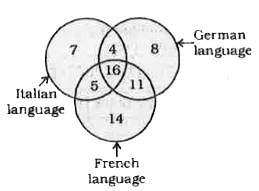 A21B16C27D20
A21B16C27D20 - Question 2 - Select One
In a group of 1000 people 700 can speak English and 500 can speak Hindi. If all the people speak atleast one of the two languages find:
(a) how many can speak both the languages?
(b) how many can speak exactly one language ?A300B200C400D500 - Question 3 - Select One
In a flight 55 people speak Hindi, 20 speak English and 15 speak both English and Hindi. The number of people who speak at least one of the two languages is
A40B50C20D60
In a group of 50 people, 35 speak Hindi, 25 speak both English and Hindi and all the people speak at least one of the two languages. How many people speak only English and not Hindi? How many people speak English?
View SolutionIn a committee, 50 people speak Hindi, 20 speak English and 10 speak both Hindi and English . How many speak at least one of these two languages ?
View SolutionIn a group of 400 persons 250 can speak Hindi and 200 can speak English. Each person speak atleast one language. Find how many persons can speak both languages ?
View SolutionIn a committee, 40 person can speak Hindi 20 can speak English and 10 can speak both languages. Find how many persons can speak atleast one language ?
View SolutionStudy the diagram and identify the people who speak only one language.
 View Solution
View Solution
