Find the mean of the distribution. 130, 90, 25, 77, 250, 100
25
77
100
112
The correct Answer is:D
To find the mean of the given distribution, we will follow these steps:
Step 1: List the Observations
The observations given are:
- 130
- 90
- 25
- 77
- 250
- 100
Step 2: Calculate the Sum of the Observations
We need to add all the observations together.
Sum=130+90+25+77+250+100
Calculating this step-by-step:
- First, add 130 and 90:
130+90=220
- Next, add 25:
220+25=245
- Then, add 77:
245+77=322
- Now, add 250:
322+250=572
- Finally, add 100:
572+100=672
So, the total sum of the observations is 672.
Step 3: Count the Number of Observations
The number of observations is 6 (as there are six numbers in the list).
Step 4: Calculate the Mean
Now, we will use the formula for the mean:
Mean=Sum of ObservationsNumber of Observations=6726
Calculating this:
- Divide 672 by 6:
672÷6=112
Conclusion
The mean of the distribution is 112.
---
The observations given are:
- 130
- 90
- 25
- 77
- 250
- 100
We need to add all the observations together.
- First, add 130 and 90:
130+90=220
- Next, add 25:
220+25=245
- Then, add 77:
245+77=322
- Now, add 250:
322+250=572
- Finally, add 100:
572+100=672
The number of observations is 6 (as there are six numbers in the list).
Now, we will use the formula for the mean:
- Divide 672 by 6:
672÷6=112
The mean of the distribution is 112.
Similar Questions
Knowledge Check
Find the mean of the following distribution:
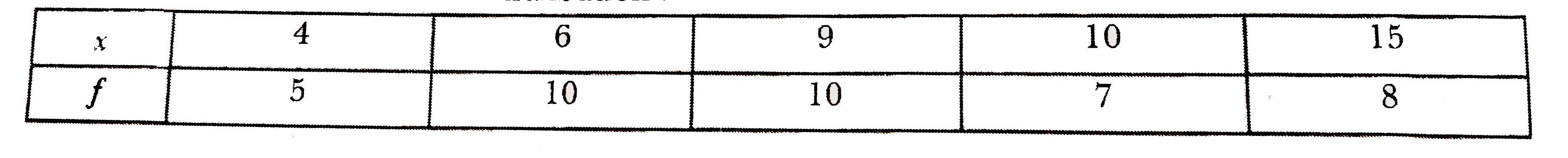 A9B10C11D12
A9B10C11D12
Find the mean of the following distribution.

View SolutionFind the mean of the following distribution.

View SolutionFind the mean of the following distribution

View SolutionFind the mean of the following distribution :

View SolutionFind the mean of data 130, 90, 25, 77, 250, 100 (A) 25 (B) 77 (C ) 112 (D) 120
View SolutionFind the mean of the following distribution:
View SolutionFind the mean of the following distribution:
View Solution

