In a circle O is the center and the length of diameter and one chord is 25 cm and 21 cm respectively. Then find the perpendicular distance from center to the chord.
(A). √46cm
(B). √23cm
(C). √21cm
(D). √34cm
The correct Answer is:A
To find the perpendicular distance from the center of the circle to the chord, we can follow these steps:
Step 1: Identify the given values
- The diameter of the circle is 25 cm.
- The length of the chord is 21 cm.
Step 2: Calculate the radius of the circle
The radius (r) is half of the diameter. Therefore:
r=Diameter2=25 cm2=12.5 cm
Step 3: Divide the chord into two equal parts
Since the perpendicular from the center of the circle to the chord bisects the chord, we can find the length of half the chord (BD):
BD=Length of chord2=21 cm2=10.5 cm
Step 4: Apply the Pythagorean theorem
In the right triangle ODB, where:
- OB is the hypotenuse (the radius of the circle),
- BD is one leg (half the chord),
- OD is the other leg (the perpendicular distance we want to find).
According to the Pythagorean theorem:
OB2=OD2+BD2
Step 5: Substitute the known values into the equation
Substituting the values we have:
(12.5)2=OD2+(10.5)2
Calculating the squares:
156.25=OD2+110.25
Step 6: Solve for OD2
Rearranging the equation to solve for OD2:
OD2=156.25−110.25=46
Step 7: Calculate OD
Taking the square root to find OD:
OD=√46 cm
Final Answer
The perpendicular distance from the center of the circle to the chord is:
OD≈6.78 cm
---
- The diameter of the circle is 25 cm.
- The length of the chord is 21 cm.
The radius (r) is half of the diameter. Therefore:
r=Diameter2=25 cm2=12.5 cm
Since the perpendicular from the center of the circle to the chord bisects the chord, we can find the length of half the chord (BD):
BD=Length of chord2=21 cm2=10.5 cm
In the right triangle ODB, where:
- OB is the hypotenuse (the radius of the circle),
- BD is one leg (half the chord),
- OD is the other leg (the perpendicular distance we want to find).
OB2=OD2+BD2
Substituting the values we have:
(12.5)2=OD2+(10.5)2
Calculating the squares:
156.25=OD2+110.25
Rearranging the equation to solve for OD2:
OD2=156.25−110.25=46
Taking the square root to find OD:
OD=√46 cm
The perpendicular distance from the center of the circle to the chord is:
OD≈6.78 cm
Similar Questions
(i) Find the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13cm.
(ii) The length of a chord is 16 cm of a circle of diameter 2 cm. find the perpendicular distance of this chord from the centre of the circle.
View SolutionIn a circle of diameter 40cm the length of a chord is 20 cm Find the length of the minor arc
View Solution
Knowledge Check
In a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cmIn a circle of diameter44 cm, the length of a chord is 22 cm. What is the length of minor arc of the chord ?
A48421 cmB24221cmC12121cmD447cmEF is a chord of a circle whose length is 10 cm. If radius of the circle is 13 cm, then the length of perpendicular from the centre to the chord is
A12 cmB8 cmC7 cmD5 cm
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
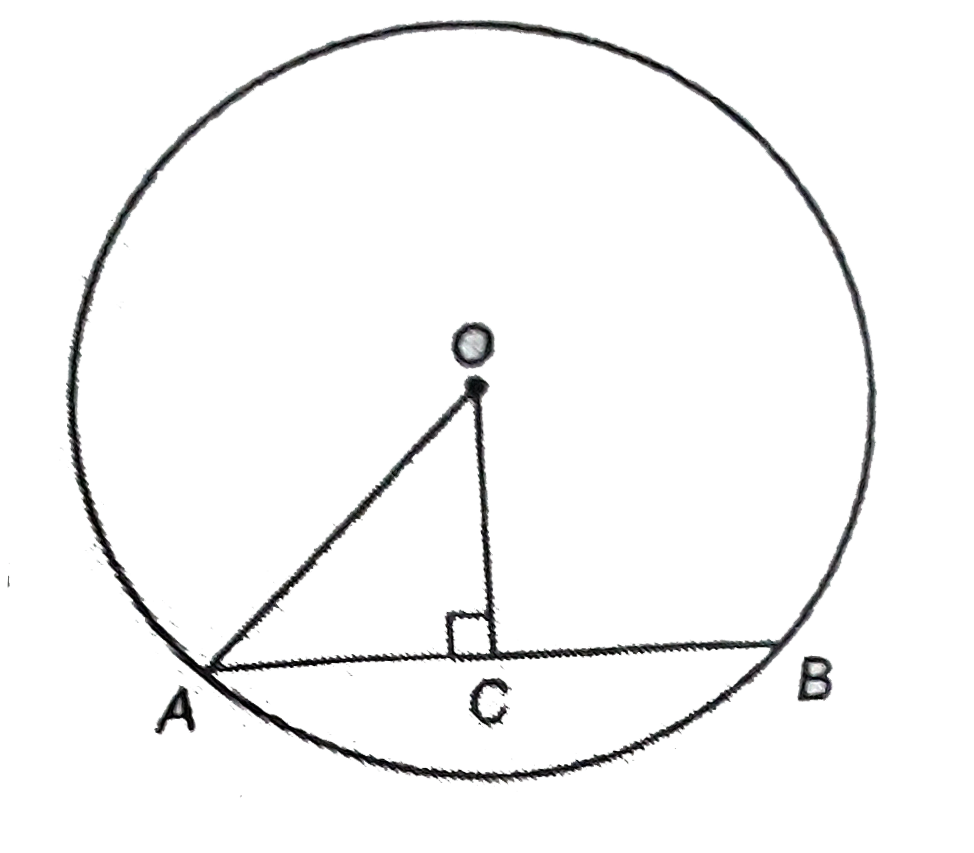
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
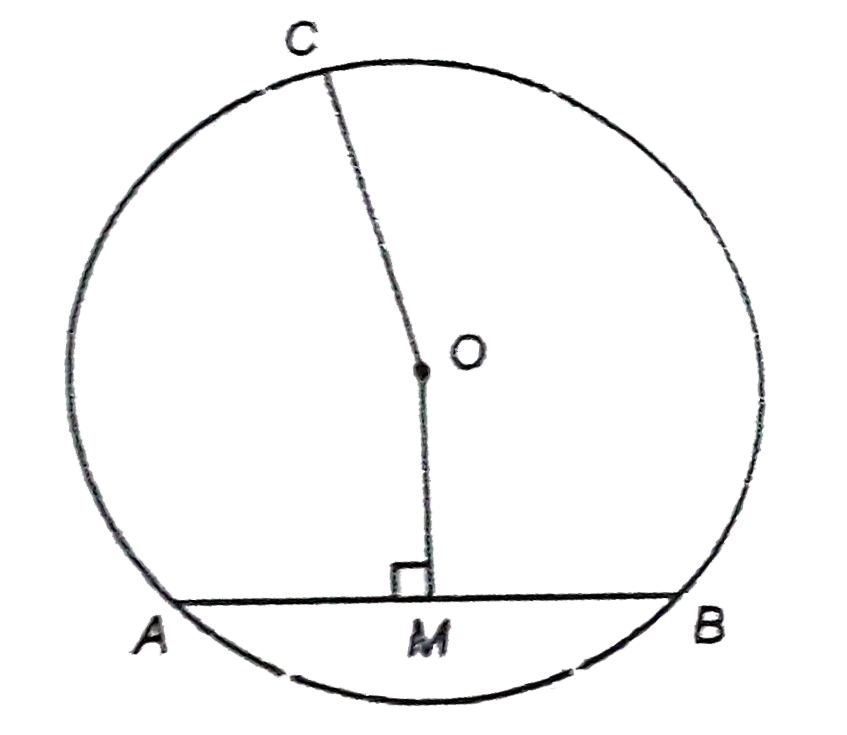
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
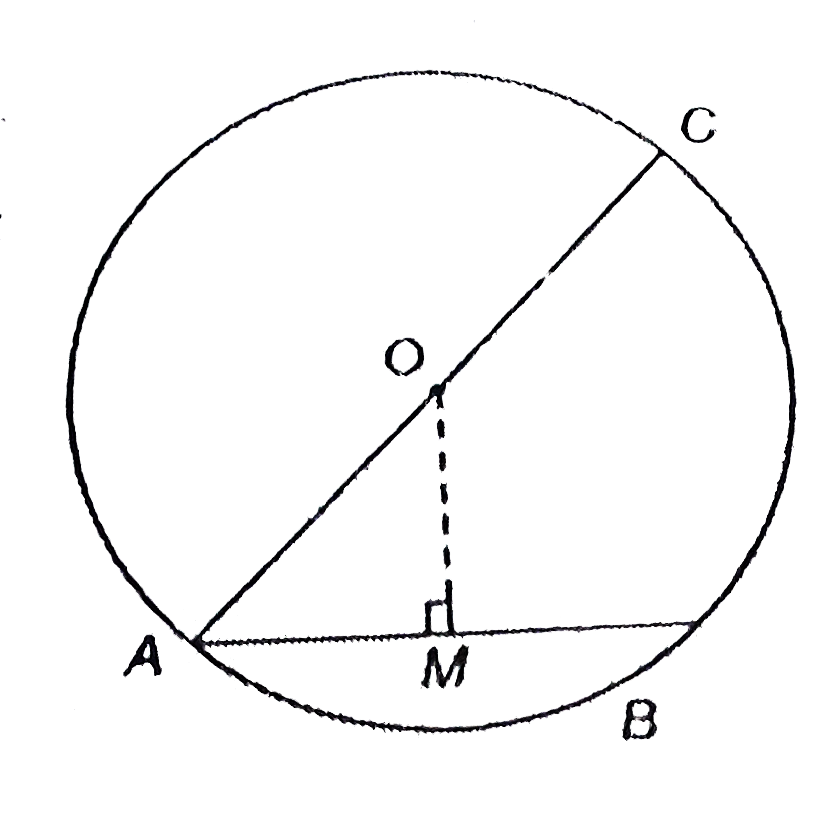
View SolutionIn a circle of diameter 40 cm. The length of a chord is 20 cm. Find the length of minor arc of the chord.
View SolutionThe radius of a circle with centere P is 25 cm . The length of a chord of the same circle is 48 cm . Find the distance of the chord from the centre P of the circle.
View SolutionThe radius of a circle is 8cm and the length of one of its chords is 12cm. Find the distance of the chord from the centre.
View Solution
